题目内容
12.解方程组$\left\{\begin{array}{l}{2x=3y①}\\{3x-2y=5②}\end{array}\right.$,按要求完成下面步骤解:由①得,x=$\frac{3}{2}$y③
把③代入②得:
3×$\frac{3}{2}$y-2y=5
整理得,$\frac{5}{2}$y=5
解得y=2
把y=2代入方程③,得x=3
∴原方程组的解是$\left\{\begin{array}{l}{x=()}\\{y=()}\end{array}\right.$.
分析 方程组变形后,利用代入消元法求出解即可.
解答 解:由①得,x=$\frac{3}{2}$y③,
把③代入②得:3×$\frac{3}{2}$y-2y=5,
整理得,$\frac{5}{2}$y=5,
解得y=2,
把y=2代入方程③,得x=3,
∴原方程组的解是$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$.
故答案为:$\frac{3}{2}$y;②;$\frac{3}{2}$y;$\frac{5}{2}$y=5;2;2;3
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列各数中最大的数是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 0 | D. | 1 |
17.若式子$\sqrt{-a-b}$+$\frac{1}{\sqrt{ab}}$有意义,则点P(a、b)在( )
| A. | 坐标原点 | B. | 第一象限 | C. | 第二象限 | D. | 第三象限 |
2.下列说法正确的是( )
| A. | 绝对值等于本身的数是正数 | B. | -a是负数 | ||
| C. | 有理数不是正数就是负数 | D. | 分数都是有理数 |
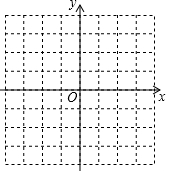 (1)在下面的平面直角坐标系中画△ABC,使△ABC各顶点坐标分别为A(2,-1),B(-2,0),C(0,-2);
(1)在下面的平面直角坐标系中画△ABC,使△ABC各顶点坐标分别为A(2,-1),B(-2,0),C(0,-2);