题目内容
10.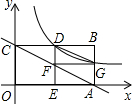 如图,已知矩形OABC中,点A(2,0)、C(0,1).点D是边BC的中点,过点D作DE⊥OA于点E,双曲线y=$\frac{k}{x}$过点D交AB于点G,直线AC交DE于点F,连接DG、FG.
如图,已知矩形OABC中,点A(2,0)、C(0,1).点D是边BC的中点,过点D作DE⊥OA于点E,双曲线y=$\frac{k}{x}$过点D交AB于点G,直线AC交DE于点F,连接DG、FG.(1)求点D的坐标;
(2)求k的值与直线AC的解析式;
(3)求四边形DCFG的面积.
分析 (1)由矩形的性质和中点的定义容易得出结果;
(2)由点D的证明求出k的值,由待定系数法求出直线AC的解析式即可;
(3)由矩形的性质得出BC=OA,BC∥OA,AB=OC=1,求出G点坐标为(2,$\frac{1}{2}$),得出G是AB的中点,证明四边形DCFG是平行四边形,即可求出面积.
解答 解:(1)∵矩形OABC中,点A(2,0)、C(0,1),点D是BC的中点,
∴D(1,1),
(2)∵点D在双曲线y=$\frac{k}{x}$上,
∴k=1×1=1,
∴反比例函数的解析式为;y=$\frac{1}{x}$.
设直线AC的解析式为y=ax+b,
根据题意得:$\left\{\begin{array}{l}{2a+b=0}\\{b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴直线AC的解析式为y=-$\frac{1}{2}$x+1;
(3)∵四边形OABC是矩形,点A(2,0),
∴BC=OA,BC∥OA,AB=OC=1,
当x=2时,y=$\frac{1}{2}$,
∴G点坐标为(2,$\frac{1}{2}$),
∴G是AB的中点,
∵点D是边BC的中点,DE⊥OA,
∴E是OA的中点,
∴CD=AE,
∵BC∥OA,
∴DF:EF=CD:AE=1:1,
∴DF=EF=$\frac{1}{2}$DE=$\frac{1}{2}$OC=$\frac{1}{2}$,
∴FG∥CD,FG=AE=CD,
∴四边形DCFG是平行四边形,
∴四边形DCFG的面积=CD•DF=1×$\frac{1}{2}$=$\frac{1}{2}$.
点评 本题考查的是反比例函数与一次函数的交点、待定系数法求函数解析式、矩形的性质、平行四边形的判定与性质等知识;熟练掌握矩形的性质,求出函数解析式是解决问题的关键.

| A. | 绝对值等于本身的数是正数 | B. | -a是负数 | ||
| C. | 有理数不是正数就是负数 | D. | 分数都是有理数 |
| -1 | ||||||
| 2 | -3 | 4 | ||||
| -5 | 6 | -7 | 8 | -9 | ||
| 10 | -11 | 12 | -13 | 14 | -15 | 16 |
| … |
| A. | 363 | B. | 364 | C. | -363 | D. | -364 |
| A. | 对角线相等,且一组对角相等的四边形是平行四边形 | |
| B. | 一对邻角的和为180°的四边形是平行四边形 | |
| C. | 一组对边平行且相等的四边形是平行四边形 | |
| D. | 两条对角线相互垂直的四边形是平行四边形 |
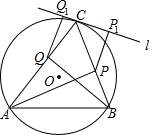 如图,过△ABC的顶点C作这个三角形的外接圆的切线l,AP和BQ即是△ABC的两条高,QQ1⊥l,PP1⊥l,求证:QQ1=PP1.
如图,过△ABC的顶点C作这个三角形的外接圆的切线l,AP和BQ即是△ABC的两条高,QQ1⊥l,PP1⊥l,求证:QQ1=PP1. 如图,∠CBD,∠ADE为△ABD的两个外角,∠CBD=70°,∠ADE=149°,则∠A的度数为39°.
如图,∠CBD,∠ADE为△ABD的两个外角,∠CBD=70°,∠ADE=149°,则∠A的度数为39°.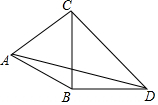 如图,△ABC是等边三角形,∠CBD=90°,BD=DC,则∠BAD的度数是15°.
如图,△ABC是等边三角形,∠CBD=90°,BD=DC,则∠BAD的度数是15°.