题目内容
9.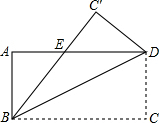 如图,将长方形ABCD沿对角线BD折叠,使C恰好落在C'位置,∠DBC=25°,则∠ABC'=40°.
如图,将长方形ABCD沿对角线BD折叠,使C恰好落在C'位置,∠DBC=25°,则∠ABC'=40°.
分析 依据正方形的性质可知∠ABC=90°,由折叠的性质可知∠C′BD=∠DBC=25°,故此可求得问题的答案.
解答 解:根据折叠的性质可知∠CBD=∠DBC′=25°.
∴∠CBC′=50°.
∵ABCD为正方形,
∴∠ABC=90°.
∴∠ABC′=∠ABC-∠CBC′=40°.
故答案为:40°.
点评 本题主要考查的是矩形的性质、翻折的性质,依据翻折的性质求得∠CBC′的度数是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
17.若式子$\sqrt{-a-b}$+$\frac{1}{\sqrt{ab}}$有意义,则点P(a、b)在( )
| A. | 坐标原点 | B. | 第一象限 | C. | 第二象限 | D. | 第三象限 |
19.我们知道:1+3=4,1+3+5=9,1+3+5+7=16,…,观察下面的一列数:-1,2,-3,4,-5,6,…将这些数排成如图的形式,根据其规律猜想:第20行第3个数是( )
| -1 | ||||||
| 2 | -3 | 4 | ||||
| -5 | 6 | -7 | 8 | -9 | ||
| 10 | -11 | 12 | -13 | 14 | -15 | 16 |
| … |
| A. | 363 | B. | 364 | C. | -363 | D. | -364 |
 如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC与点E.则$\widehat{DE}$的度数为34°.
如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC与点E.则$\widehat{DE}$的度数为34°.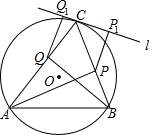 如图,过△ABC的顶点C作这个三角形的外接圆的切线l,AP和BQ即是△ABC的两条高,QQ1⊥l,PP1⊥l,求证:QQ1=PP1.
如图,过△ABC的顶点C作这个三角形的外接圆的切线l,AP和BQ即是△ABC的两条高,QQ1⊥l,PP1⊥l,求证:QQ1=PP1.