题目内容
11.已知n是正整数,则奇数可以用代数式2n+1来表示(1)分解因式:(2n+1)2-1;
(2)我们把所有“奇数的平方减去1”所得的数叫“白银数”,则所有“白银数”的最大公约数是多少?请简要说明理由.
分析 (1)原式利用平方差公式分解即可;
(2)根据(1)的结果,利用“白银数”的定义判断出所有“白银数”的最大公约数即可.
解答 解:(1)原式=(2n+1+1)(2n+1-1)=2n(2n+2)=4n(n+1);
(2)所有“白银数”的最大公约数是4,理由为:
证明:∵(2n+1)2-1=4n(n+1),
∴所有“白银数”的最大公约数是4.
点评 此题考查了因式分解-运用公式法,以及新定义,熟练掌握平方差公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列各数中最大的数是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 0 | D. | 1 |
6.如果x=2是方程2x+a=-1的解,那么a的值是( )
| A. | 0 | B. | 3 | C. | -2 | D. | -5 |
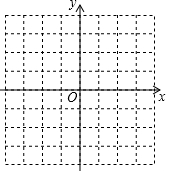 (1)在下面的平面直角坐标系中画△ABC,使△ABC各顶点坐标分别为A(2,-1),B(-2,0),C(0,-2);
(1)在下面的平面直角坐标系中画△ABC,使△ABC各顶点坐标分别为A(2,-1),B(-2,0),C(0,-2);