题目内容
9.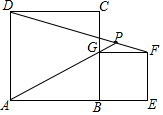 如图,正方形ABCD边长为a,正方形BEFG边长为b,A、B、E在同一直线上,两个正方形在同侧,连AG与DF交于P.
如图,正方形ABCD边长为a,正方形BEFG边长为b,A、B、E在同一直线上,两个正方形在同侧,连AG与DF交于P.(1)如a=2,b=1,则DF=$\sqrt{10}$;
(2)如a=2,b是一个变量,在b的变化过程中,动点P运动的路径为$\frac{\sqrt{2}}{2}$π.
分析 (1)如图1中,延长FG交AD于H,则四边形ABGH是矩形,在Rt△DFH中,利用勾股定理即可解决问题;
(2)如图2中,连接BD、BF,BD交AG于K.由△DBF∽△ABG,推出∠BAG=∠BDF,由∠AKB=∠DKP,推出∠DPA=∠ABK=45°,连接AC交BD于O,易知点P在以O为圆心,OA为半径的圆上运动,运动路径是$\widehat{BC}$,由此即可解决问题.
解答 解:(1)如图1中,延长FG交AD于H,则四边形ABGH是矩形,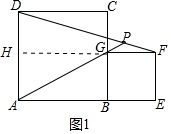
在Rt△DFH中,∵DH=AD=AH=2-1=1,FH=2+1=3,
∴DF=$\sqrt{D{H}^{2}+H{F}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$.
故答案为$\sqrt{10}$.
(2)如图2中,连接BD、BF,BD交AG于K.
∵四边形ABCD是正方形,四边形EFGB是正方形,
∴BD=$\sqrt{2}$AB,BF=$\sqrt{2}$BG,∠DBC=∠FBG=45°,
∴∠ABG=∠DBF=90°,
∴$\frac{BD}{BA}$=$\frac{BF}{BG}$=$\sqrt{2}$,
∴△DBF∽△ABG,
∴∠BAG=∠BDF,
∵∠AKB=∠DKP,
∴∠DPA=∠ABK=45°,
连接AC交BD于O,易知点P在以O为圆心,OA为半径的圆上运动,运动路径是$\widehat{BC}$,
∵OC=OB=$\sqrt{2}$,∠COB=90°
∴$\widehat{BC}$的长=$\frac{90•π•\sqrt{2}}{180}$=$\frac{\sqrt{2}}{2}$π.
故答案为$\frac{\sqrt{2}}{2}$π.
点评 本题考查正方形的性质、勾股定理、相似三角形的判定和性质、轨迹、圆等知识,解题的关键是正确寻找点P的运动轨迹,题目比较难,属于中考压轴题.

 名校课堂系列答案
名校课堂系列答案| A. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | ($\sqrt{5}$)2=25 | D. | $\sqrt{16}$=±4 |
| A. | x≠0 | B. | x≠1 | C. | x≥1 | D. | x≤1 |
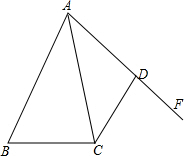 如图,己知AB>AD,∠BAC=∠FAC,CD=BC,求证:∠ADC+∠B=180°.
如图,己知AB>AD,∠BAC=∠FAC,CD=BC,求证:∠ADC+∠B=180°.
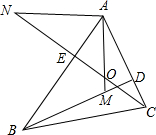 如图,在△ABC中,CE,BD为高线,M、N在BD,CE(或延长线上),且BM=AC,CN=AB.
如图,在△ABC中,CE,BD为高线,M、N在BD,CE(或延长线上),且BM=AC,CN=AB.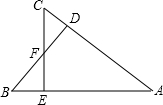 已知:如图,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点F,
已知:如图,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点F,