题目内容
19.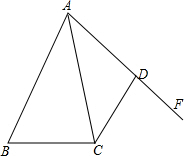 如图,己知AB>AD,∠BAC=∠FAC,CD=BC,求证:∠ADC+∠B=180°.
如图,己知AB>AD,∠BAC=∠FAC,CD=BC,求证:∠ADC+∠B=180°.
分析 作CF⊥AD交AD的延长线于F,CE⊥AB交AB的于E,根据角平分线的性质得到CE=CF,证明Rt△BEC≌Rt△DFC,根据全等三角形的性质证明结论.
解答 证明:作CF⊥AD交AD的延长线于F,CE⊥AB交AB的于E,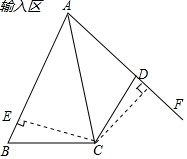
∵∠BAC=∠FAC,
∴AC平分∠BAD,
∵CE⊥AB,CF⊥AD,
∴CE=CF,
∵CD=BC,
在Rt△BEC和Rt△DFC中,
$\left\{\begin{array}{l}{CE=CF}\\{CD=BC}\end{array}\right.$,
∴Rt△BEC≌Rt△DFC,
∴∠B=∠CDF,
∵∠ADC+∠CDF=180°,
∴∠ADC+∠B=180°,
点评 本题考查的是角平分线的性质和三角形全等的判定和性质,掌握角的平分线上的点到角的两边的距离相等、灵活运用三角形全等的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
 用5个完全相同的小正方体组成如图所示的立体图形,将右上角的小正方体拿掉后俯视图为( )
用5个完全相同的小正方体组成如图所示的立体图形,将右上角的小正方体拿掉后俯视图为( )



 如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )
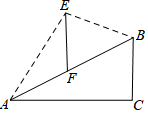
如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( ) 已知:如图,E,B,F,C四点在同一直线上,∠A=∠D=90°,BE=FC,AB=DF.
已知:如图,E,B,F,C四点在同一直线上,∠A=∠D=90°,BE=FC,AB=DF.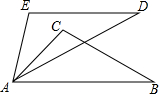 如图,AE=AC,∠E=∠C=80°,ED=CB,∠D=40°,∠CAD=35°,则∠BAE的度数是85°.
如图,AE=AC,∠E=∠C=80°,ED=CB,∠D=40°,∠CAD=35°,则∠BAE的度数是85°.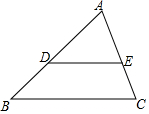 如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$,AB=12,AE=6,EC=4.则AD=$\frac{36}{5}$.
如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$,AB=12,AE=6,EC=4.则AD=$\frac{36}{5}$.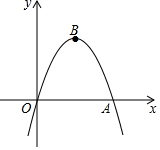 如图,在平面直角坐标系中,抛物线y=-x2+bx与x轴正半轴交于点A,顶点为B,当存在以AB为边,以点O为对称中心的矩形时,b的值为2$\sqrt{3}$.
如图,在平面直角坐标系中,抛物线y=-x2+bx与x轴正半轴交于点A,顶点为B,当存在以AB为边,以点O为对称中心的矩形时,b的值为2$\sqrt{3}$.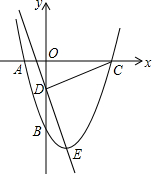 如图,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).
如图,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).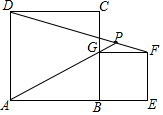 如图,正方形ABCD边长为a,正方形BEFG边长为b,A、B、E在同一直线上,两个正方形在同侧,连AG与DF交于P.
如图,正方形ABCD边长为a,正方形BEFG边长为b,A、B、E在同一直线上,两个正方形在同侧,连AG与DF交于P.