题目内容
19.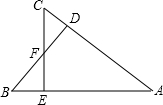 已知:如图,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点F,
已知:如图,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点F,(1)若FC=FB,证明AF平分∠BAC.
(2)若点F在∠BAC的平分线上,证明FC=FB.
分析 (1)连接AF,如图,根据“AAS”证明△BEF≌△CDF,从而得到FE=FD,然后根据角平分线的性质定理可得到AF平分∠BAC;
(2)根据角平分线的性质定理可得FE=FD,则可根据“ASA“证明△BEF≌△CDF,从而得到BF=CF.
解答 证明:(1)连接AF,如图,
∵BD⊥AC,CE⊥AB,
∴∠CEB=∠BDC=90°,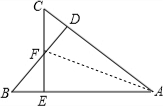
在△BEF和△CDF中
$\left\{\begin{array}{l}{∠BFE=∠CFD}\\{∠BEF=∠CDF}\\{BF=CF}\end{array}\right.$,
∴△BEF≌△CDF,
∴FE=FD,
而FE⊥AB,FD⊥AC,
∴AF平分∠BAC;
(2)∵点F在∠BAC的平分线上,FE⊥AB,FD⊥AC,
∴FE=FD,
在△BEF和△CDF中
$\left\{\begin{array}{l}{∠BFE=∠CFD}\\{FE=FD}\\{∠BEF=∠CDF}\end{array}\right.$,
∴△BEF≌△CDF,
∴BF=CF.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.也考查了角平分线的性质定理.

练习册系列答案
相关题目
8.在Rt△ABC中,斜边AB上的中线CD为4cm,则斜边AB的长为( )
| A. | 2cm | B. | 12cm | C. | 8cm | D. | 16cm |
9.下列实数是无理数的是( )
| A. | $\sqrt{2}$ | B. | 3.14 | C. | $\frac{22}{7}$ | D. | 38 |
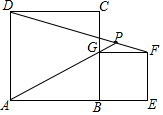 如图,正方形ABCD边长为a,正方形BEFG边长为b,A、B、E在同一直线上,两个正方形在同侧,连AG与DF交于P.
如图,正方形ABCD边长为a,正方形BEFG边长为b,A、B、E在同一直线上,两个正方形在同侧,连AG与DF交于P.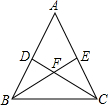 如图,等腰△ABC中,AB=AC,CD,BE是两腰上的高,说明CD=BE.
如图,等腰△ABC中,AB=AC,CD,BE是两腰上的高,说明CD=BE.