题目内容
如图,△ABC关于直线L的轴对称图形是△DEF, 如果△ABC的面积为6CM2,且DE=3CM， 求△ABC中AB边上的高h.
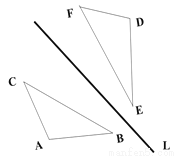
h=4cm
【解析】试题分析：本题思路的关键是利用轴对称图形的性质，得到AB =DE=3cm，然后利用面积法求出AB边上的高h.
【解析】
∵△ABC关于直线L的轴对称图形是△DEF，
∴AB =DE=3cm，
∴h=6×2÷3=4cm.
练习册系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
已知：如图，△ABC中，D是BC边的中点，AE平分∠BAC，BE⊥AE于E点，若AB＝5，AC＝7，求ED．
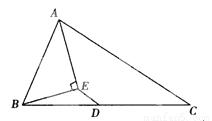
ED=1.
【解析】延长BE交AC于F，
∵AE平分∠BAC，
∴∠BAE＝∠CAE，
∵BE⊥AE，AE＝AE，
∴△ABE≌△AFE，
∴AF＝AB，BE＝EF，
∵AB＝5，
∴AF＝5，
∵AC＝7，
∴CF＝AC-AF＝7-5＝2，
∵D为BC中点，
∴BD＝CD，
∴DE是△BCF的中位线，
∴DE＝C... 下面给出的5个式子中：①3＞0，②4x+3y＞0，③x=3，④x－1，⑤x+2≤3，其中不等式有（ ）
A．2个 B．3个 C．4个 D．5个
B．
【解析】
试题解析：3＞0；4x+3y＞0；x+2≤3是不等式．
故选B． 下列命题中，正确的是( )
A. 两个全等的三角形合在一起是一个轴对称图形
B. 等腰三角形的对称轴是底边上的中线
C. 等腰三角形底边上的高就是底边的垂直平分线
D. 一条线段可以看做以它的垂直平分线为对称轴的轴对称图形
D
【解析】A两个全等三角形合在一起不一定是轴对称图形，需要看实际组合成什么样的图形；
B中应该为底边上的中线所在的直线；
C应该是底边的垂直平分线被三角形所截取的线段；
故此题正确选项为D. 对于下列命题：（1）关于某一直线成轴对称的两个三角形全等；（2）等腰三角形的对称轴是顶角的平分线；（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点；（4）如果两个三角形全等，那么它们关于某直线成轴对称。其中真命题的个数为
A、0 B、1 C、2 D、3
C
【解析】
试题分析：根据平面图形的基本概念依次分析各小题即可作出判断.
（1）关于某一直线成轴对称的两个三角形全等，（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点，均为真命题；
（2）等腰三角形的对称轴是顶角的平分线所在的直线，（4）如果两个三角形全等，它们可能是平移或旋转构成的，均为假命题；
故选C. 若直角三角形是轴对称图形,则其三个内角的度数分别为________.
90°45°45°
【解析】∵直角三角形是轴对称图形 ，
∴一定有两个角相等.
又∵直角三角形一定有一个角为90°，
∴相等的是两个锐角.
∵直角三角形的两个锐角互余，
∴每一个锐角为45°. 下面说法中正确的是( )
A. 设A、B关于直线MN对称，则AB垂直平分MN.
B. 如果△ABC≌△DNF,则一定存在一条直线MN，使△ABC与△DNF关于MN 对称.
C. 如果一个三角形是轴对称图形，且对称轴不止一条，则它是等边三角形.
D. 两个图形关于MN对称，则这两个图形分别在MN的两侧.
C
【解析】A中应该是直线MN垂直平分线段AB，故错误；
B因为成轴对称的两个图形一定全等，但全等形不一定是轴对称图形，故错误；
C因为等边三角形是轴对称图形，且有3条对称轴，故正确；
D中错在这两个图形不一定要在直线两侧，同侧也可以有，如下图，故错误.
故选C. 用边长为4cm，5cm，6cm的两个全等三角形一共能拼成__________个平行四边形．
3
【解析】【解析】
如图所示：
共6个四边形，其中有3个平行四边形．
故答案为：3． 若代数式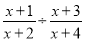
有意义，则x的取值范围是________
，
【解析】试题解析：因为x+2≠0，且x+4≠0，所以x≠?2且x≠?4.
又0作除数无意义，所以x+3≠0，即x≠?3.
故空中填：x≠?2，?3，?4.
故答案为： ， 且.