题目内容
若直角三角形是轴对称图形,则其三个内角的度数分别为________.
90°45°45°
【解析】∵直角三角形是轴对称图形 ，
∴一定有两个角相等.
又∵直角三角形一定有一个角为90°，
∴相等的是两个锐角.
∵直角三角形的两个锐角互余，
∴每一个锐角为45°.
练习册系列答案
相关题目
如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，求证：四边形EFGH是平行四边形。
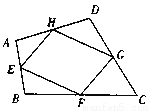
证明见解析
【解析】试题分析：连接AC，根据三角形的中位线的性质证得线段平行且相等，从而根据平行四边形的判定（一组对边平行且相等的四边形是平行四边形）得证.
试题解析：证明：连接AC
∵E，F，G，H是四边形ABCD的中点
∴EF，HG分别是△BCA和△DCA的中位线
∴EF∥AC，HG∥AC，且EF=
∴EF∥HG， EF=HG
∴四边形EFGH是平行四... 画出所示⊿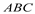
关于直线l对称的⊿
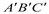(保留痕迹)
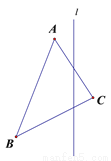
见解析
【解析】根据画轴对称图形的方法即可得出答案.
作法：如图所示，
1.作点△的三个顶点A、B、C关于直线l对称的点A’、B’、C’；
2.顺次连结A’B’、 B’ C’、C’ A’得⊿A’B’C.
则△A’B’C即为所求作的三角形. 下列图案中，不能用折叠剪纸方法得到的是( ）
A. B. C. D.
C
【解析】根据轴对称图形的定义即可解答.
【解析】
由给出的图案，结合轴对称的性质，可知C是旋转一定的角度后与原来的图案对称的，不是一个轴对称图形，故选C. 如图,△ABC关于直线L的轴对称图形是△DEF, 如果△ABC的面积为6CM2,且DE=3CM， 求△ABC中AB边上的高h.
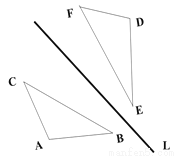
h=4cm
【解析】试题分析：本题思路的关键是利用轴对称图形的性质，得到AB =DE=3cm，然后利用面积法求出AB边上的高h.
【解析】
∵△ABC关于直线L的轴对称图形是△DEF，
∴AB =DE=3cm，
∴h=6×2÷3=4cm. 下列推理中，错误的是( )
A. ∵∠A＝∠B＝∠C，∴△ABC是等边三角形
B. ∵AB＝AC，且∠B＝∠C，∴△ABC是等边三角形
C. ∵∠A＝60°，∠B＝60°，∴△ABC是等边三角形
D. ∵AB＝AC，∠B＝60°，∴△ABC是等边三角形
B
【解析】A∵∠A＝∠B＝∠C，∴△ABC是等边三角形，故正确；
B条件重复且条件不足，故不正确；
C∵∠A＝60°，∠B＝60°，∴∠C=60°，∴△ABC是等边三角形60°，故正确；
D根据有一个角是60°的等腰三角形是等边三角形可以得到，故正确.
故选B. 如图所示，在桌面上坚直放置两块镜面相对的平面镜，在两镜之间放一个小凳，那么在两镜中共可得到小凳的像( )
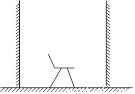
A. 2个 B. 4个 C. 16个 D. 无数个
D
【解析】∵两块镜面相对，
∴在每一块镜面中，都能有对方镜面的图像，
∴小凳在每一个镜面中都有图像.
∵每一个面中的小凳都在对面镜子中有图像，
∴循环往复，图像无数.
故选D 如图：在4×4的正方形（每个小正方形的边长均为1）网格中，以A为顶点，其他三个顶点都在格点（网格的交点）上，且面积为2的平行四边形的共有（ ）个．
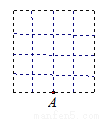
A. 10 B. 12 C. 14 D. 23
D
【解析】【解析】
一顶点在BC上，两顶点在MG上的有四边形AGIB、AOQB、AMIF、AQFO、ABMI、AFGI共6个；
一顶点在BC上，两顶点在PH上的有四边形AHVC、AVNC、APZE、AZNE、AEVN、ACZN共6个；
还有四边形AQNO、AIYL、ATXI、AHLI、APTI、AGHI、AMPI、AZRN、AVR′N、AOKN、AQSN，共11个；
... 分式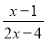
的值为零的条件是____________
【解析】试题解析：：因为分式的值为0的时候，只能是分子为0，分母不能为0，所以可以得到， ；可以得到且
故答案为： .