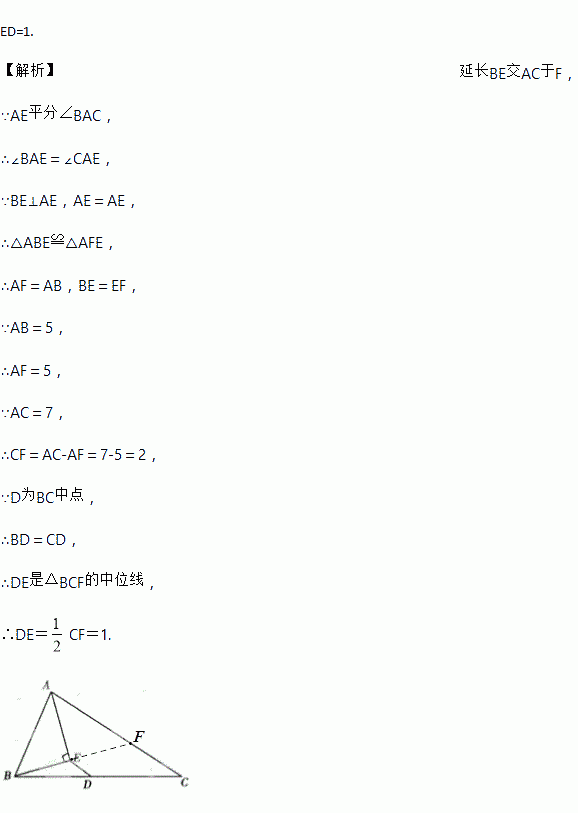题目内容
已知:如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,求ED.
 ED=1.
【解析】延长BE交AC于F,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵BE⊥AE,AE=AE,
∴△ABE≌△AFE,
∴AF=AB,BE=EF,
∵AB=5,
∴AF=5,
∵AC=7,
∴CF=AC-AF=7-5=2,
∵D为BC中点,
∴BD=CD,
∴DE是△BCF的中位线,
∴DE=C...
ED=1.
【解析】延长BE交AC于F,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵BE⊥AE,AE=AE,
∴△ABE≌△AFE,
∴AF=AB,BE=EF,
∵AB=5,
∴AF=5,
∵AC=7,
∴CF=AC-AF=7-5=2,
∵D为BC中点,
∴BD=CD,
∴DE是△BCF的中位线,
∴DE=C...
练习册系列答案
相关题目
已知:如图,AD是△ABC的高,E是AD上一点,BE的延长线交AC于点F,BE=AC,DE=DC,BE和AC垂直吗?说明理由.
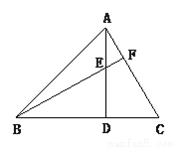
 BE⊥AC
【解析】试题分析:在直角△BED与△ACD中,根据HL判定△BED≌ACD,根据全等三角形的对应角相等,得出∠DBE=∠DAC,再根据AD是高线,结合∠BED=∠AEF,进而推出∠DAC+∠AEF=90°,据此可得结论.
试题解析:BF⊥AC.理由如下:
∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵在直角△BED与△ACD中,BE=AC,DE...
BE⊥AC
【解析】试题分析:在直角△BED与△ACD中,根据HL判定△BED≌ACD,根据全等三角形的对应角相等,得出∠DBE=∠DAC,再根据AD是高线,结合∠BED=∠AEF,进而推出∠DAC+∠AEF=90°,据此可得结论.
试题解析:BF⊥AC.理由如下:
∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵在直角△BED与△ACD中,BE=AC,DE... 下列分式中,当x=1时,有意义的是( )
①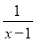 ;②
;②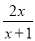 ;③
;③ ;④
;④ .
.
A. ①③ B. ①②③ C. ②③ D. ②④
 D
【解析】对于①,要使有意义,则x-1≠0,则x≠1;
对于②,要使有意义,则x+1≠0,则x≠-1;
对于③,要使有意义,则(x-1)(x-2)≠0,即x≠1且x≠2;
对于④,要使.)有意义,则(x+1)(x+2)≠0,则x≠-1且x≠-2.
综上所述,当x=1时,分式、有意义.故选D.
D
【解析】对于①,要使有意义,则x-1≠0,则x≠1;
对于②,要使有意义,则x+1≠0,则x≠-1;
对于③,要使有意义,则(x-1)(x-2)≠0,即x≠1且x≠2;
对于④,要使.)有意义,则(x+1)(x+2)≠0,则x≠-1且x≠-2.
综上所述,当x=1时,分式、有意义.故选D. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为______.
 6
【解析】∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形是六边形,
故答案为:6.
6
【解析】∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形是六边形,
故答案为:6. 已知:如图,AB∥CD,求图形中的x的值.
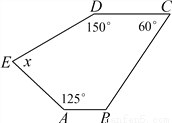
 x=85°
【解析】试题分析:先根据平行线的性质求得∠B的度数,再利用多边形的内角和定理进行求解即可.
试题解析:∵AB∥CD,∠C=60°,
∴∠B=180°-60°=120°,
∴(5-2)×180°=x+150°+125°+60°+120°,
∴x=85°.
x=85°
【解析】试题分析:先根据平行线的性质求得∠B的度数,再利用多边形的内角和定理进行求解即可.
试题解析:∵AB∥CD,∠C=60°,
∴∠B=180°-60°=120°,
∴(5-2)×180°=x+150°+125°+60°+120°,
∴x=85°. 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,求证:四边形EFGH是平行四边形。
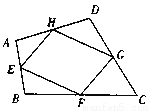
 证明见解析
【解析】试题分析:连接AC,根据三角形的中位线的性质证得线段平行且相等,从而根据平行四边形的判定(一组对边平行且相等的四边形是平行四边形)得证.
试题解析:证明:连接AC
∵E,F,G,H是四边形ABCD的中点
∴EF,HG分别是△BCA和△DCA的中位线
∴EF∥AC,HG∥AC,且EF=
∴EF∥HG, EF=HG
∴四边形EFGH是平行四...
证明见解析
【解析】试题分析:连接AC,根据三角形的中位线的性质证得线段平行且相等,从而根据平行四边形的判定(一组对边平行且相等的四边形是平行四边形)得证.
试题解析:证明:连接AC
∵E,F,G,H是四边形ABCD的中点
∴EF,HG分别是△BCA和△DCA的中位线
∴EF∥AC,HG∥AC,且EF=
∴EF∥HG, EF=HG
∴四边形EFGH是平行四... 如图,△ABC的中线BE,CF相交于点G,P、Q分别是BG、CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请直接写出BG与GE的数量关系.(不要求证明).
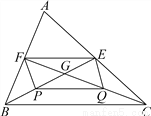
 (1)证明见解析;(2)BG=2GE.
【解析】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是...
(1)证明见解析;(2)BG=2GE.
【解析】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是... 用适当的符号表示下列关系:
(l)a的2倍比a与3的和小; (2)y的一半与5的差是非负数;
(3)x的3倍与1的和小于x的2倍与5的差.
 (1)2a<a+3;(2)y-5≥0;(3)3x+1< 2x-5
【解析】试题分析:(1)首先表示出a的2倍为2a,再表示a与3的和a+3,再利用不等式表示即可;
(2)首先表示y的一半为y,再表示与5的差为y-5,然后表示非负数即可;
(3)x的3倍与1的和表示为3x+1,x的2倍与5的差表示为2x-5,然后再抓住关键词“小于”列出不等式即可.
试题解析:(1)a的2倍为...
(1)2a<a+3;(2)y-5≥0;(3)3x+1< 2x-5
【解析】试题分析:(1)首先表示出a的2倍为2a,再表示a与3的和a+3,再利用不等式表示即可;
(2)首先表示y的一半为y,再表示与5的差为y-5,然后表示非负数即可;
(3)x的3倍与1的和表示为3x+1,x的2倍与5的差表示为2x-5,然后再抓住关键词“小于”列出不等式即可.
试题解析:(1)a的2倍为... 如图,△ABC关于直线L的轴对称图形是△DEF, 如果△ABC的面积为6CM2,且DE=3CM, 求△ABC中AB边上的高h.
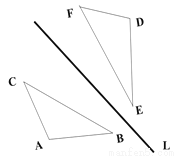
 h=4cm
【解析】试题分析:本题思路的关键是利用轴对称图形的性质,得到AB =DE=3cm,然后利用面积法求出AB边上的高h.
【解析】
∵△ABC关于直线L的轴对称图形是△DEF,
∴AB =DE=3cm,
∴h=6×2÷3=4cm.
h=4cm
【解析】试题分析:本题思路的关键是利用轴对称图形的性质,得到AB =DE=3cm,然后利用面积法求出AB边上的高h.
【解析】
∵△ABC关于直线L的轴对称图形是△DEF,
∴AB =DE=3cm,
∴h=6×2÷3=4cm.