题目内容
下面给出的5个式子中:①3>0,②4x+3y>0,③x=3,④x-1,⑤x+2≤3,其中不等式有( )
A.2个 B.3个 C.4个 D.5个
 B.
【解析】
试题解析:3>0;4x+3y>0;x+2≤3是不等式.
故选B.
B.
【解析】
试题解析:3>0;4x+3y>0;x+2≤3是不等式.
故选B.
练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
下列分式中,当x=1时,有意义的是( )
①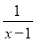 ;②
;②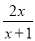 ;③
;③ ;④
;④ .
.
A. ①③ B. ①②③ C. ②③ D. ②④
 D
【解析】对于①,要使有意义,则x-1≠0,则x≠1;
对于②,要使有意义,则x+1≠0,则x≠-1;
对于③,要使有意义,则(x-1)(x-2)≠0,即x≠1且x≠2;
对于④,要使.)有意义,则(x+1)(x+2)≠0,则x≠-1且x≠-2.
综上所述,当x=1时,分式、有意义.故选D.
D
【解析】对于①,要使有意义,则x-1≠0,则x≠1;
对于②,要使有意义,则x+1≠0,则x≠-1;
对于③,要使有意义,则(x-1)(x-2)≠0,即x≠1且x≠2;
对于④,要使.)有意义,则(x+1)(x+2)≠0,则x≠-1且x≠-2.
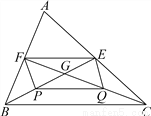
综上所述,当x=1时,分式、有意义.故选D. 如图,△ABC的中线BE,CF相交于点G,P、Q分别是BG、CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请直接写出BG与GE的数量关系.(不要求证明).
 (1)证明见解析;(2)BG=2GE.
【解析】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是...
(1)证明见解析;(2)BG=2GE.
【解析】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是... 用适当的符号表示下列关系:
(l)a的2倍比a与3的和小; (2)y的一半与5的差是非负数;
(3)x的3倍与1的和小于x的2倍与5的差.
 (1)2a<a+3;(2)y-5≥0;(3)3x+1< 2x-5
【解析】试题分析:(1)首先表示出a的2倍为2a,再表示a与3的和a+3,再利用不等式表示即可;
(2)首先表示y的一半为y,再表示与5的差为y-5,然后表示非负数即可;
(3)x的3倍与1的和表示为3x+1,x的2倍与5的差表示为2x-5,然后再抓住关键词“小于”列出不等式即可.
试题解析:(1)a的2倍为...
(1)2a<a+3;(2)y-5≥0;(3)3x+1< 2x-5
【解析】试题分析:(1)首先表示出a的2倍为2a,再表示a与3的和a+3,再利用不等式表示即可;
(2)首先表示y的一半为y,再表示与5的差为y-5,然后表示非负数即可;
(3)x的3倍与1的和表示为3x+1,x的2倍与5的差表示为2x-5,然后再抓住关键词“小于”列出不等式即可.
试题解析:(1)a的2倍为... 如果a+b<0,且b>0,那么a,b,-a,-b的大小关系为( ).
A. a<b<-a<-b
B. -b<a<-a<b
C. a<-b<-a<b
D. a<-b<b<-a
 D
【解析】∵a+b<0,且b>0,
∴a<0,|a|>b,a
D
【解析】∵a+b<0,且b>0,
∴a<0,|a|>b,a 画出所示⊿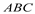 关于直线l对称的⊿
关于直线l对称的⊿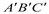 (保留痕迹)
(保留痕迹)
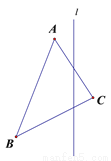
 见解析
【解析】根据画轴对称图形的方法即可得出答案.
作法:如图所示,
1.作点△的三个顶点A、B、C关于直线l对称的点A’、B’、C’;
2.顺次连结A’B’、 B’ C’、C’ A’得⊿A’B’C.
则△A’B’C即为所求作的三角形.
见解析
【解析】根据画轴对称图形的方法即可得出答案.
作法:如图所示,
1.作点△的三个顶点A、B、C关于直线l对称的点A’、B’、C’;
2.顺次连结A’B’、 B’ C’、C’ A’得⊿A’B’C.
则△A’B’C即为所求作的三角形. 若一个三角形是轴对称图形,则这个三角形一定是( )
A. 等边三角形 B. 不等边三角形 C. 等腰三角形 D. 等腰直角三角形
 C
【解析】根据轴对称图形的性质即可得出答案.
A等边三角形一定是轴对称图形,但轴对称三角形不一定是等边三角形;
B不等边三角形一定不是轴对称图形;
C等腰三角形一定是轴对称三角形;
D等腰直角三角形一定是轴对称图形,但是轴对称三角形不一定是等腰直角三角形.故选C.
C
【解析】根据轴对称图形的性质即可得出答案.
A等边三角形一定是轴对称图形,但轴对称三角形不一定是等边三角形;
B不等边三角形一定不是轴对称图形;
C等腰三角形一定是轴对称三角形;
D等腰直角三角形一定是轴对称图形,但是轴对称三角形不一定是等腰直角三角形.故选C. 如图,△ABC关于直线L的轴对称图形是△DEF, 如果△ABC的面积为6CM2,且DE=3CM, 求△ABC中AB边上的高h.
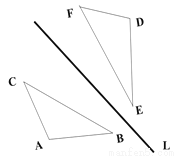
 h=4cm
【解析】试题分析:本题思路的关键是利用轴对称图形的性质,得到AB =DE=3cm,然后利用面积法求出AB边上的高h.
【解析】
∵△ABC关于直线L的轴对称图形是△DEF,
∴AB =DE=3cm,
∴h=6×2÷3=4cm.
h=4cm
【解析】试题分析:本题思路的关键是利用轴对称图形的性质,得到AB =DE=3cm,然后利用面积法求出AB边上的高h.
【解析】
∵△ABC关于直线L的轴对称图形是△DEF,
∴AB =DE=3cm,
∴h=6×2÷3=4cm. 点A、B、C是平面内不在同一条直线上的三点,点D是平面内任意一点,若A、B、C、D四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有( )
A.1个 B.2个 C.3个 D.4个
 C.
【解析】
试题分析:如图,在一个平面内,不在同一条直线上的三点,与D点恰能构成一个平行四边形,符合这样条件的点D有3个.故答案选C.
C.
【解析】
试题分析:如图,在一个平面内,不在同一条直线上的三点,与D点恰能构成一个平行四边形,符合这样条件的点D有3个.故答案选C.