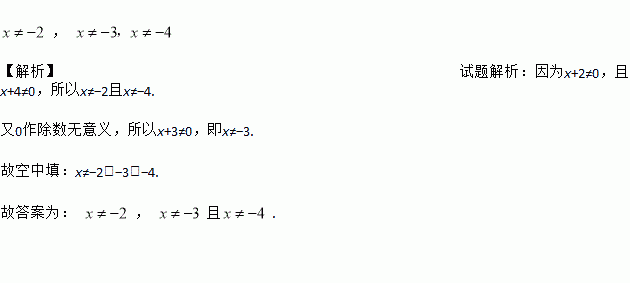题目内容
若代数式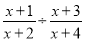 有意义,则x的取值范围是________
有意义,则x的取值范围是________
 ,
【解析】试题解析:因为x+2≠0,且x+4≠0,所以x≠?2且x≠?4.
又0作除数无意义,所以x+3≠0,即x≠?3.
故空中填:x≠?2,?3,?4.
故答案为: , 且.
,
【解析】试题解析:因为x+2≠0,且x+4≠0,所以x≠?2且x≠?4.
又0作除数无意义,所以x+3≠0,即x≠?3.
故空中填:x≠?2,?3,?4.
故答案为: , 且.
练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
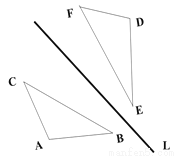
如图,△ABC关于直线L的轴对称图形是△DEF, 如果△ABC的面积为6CM2,且DE=3CM, 求△ABC中AB边上的高h.
 h=4cm
【解析】试题分析:本题思路的关键是利用轴对称图形的性质,得到AB =DE=3cm,然后利用面积法求出AB边上的高h.
【解析】
∵△ABC关于直线L的轴对称图形是△DEF,
∴AB =DE=3cm,
∴h=6×2÷3=4cm.
h=4cm
【解析】试题分析:本题思路的关键是利用轴对称图形的性质,得到AB =DE=3cm,然后利用面积法求出AB边上的高h.
【解析】
∵△ABC关于直线L的轴对称图形是△DEF,
∴AB =DE=3cm,
∴h=6×2÷3=4cm. 点A、B、C是平面内不在同一条直线上的三点,点D是平面内任意一点,若A、B、C、D四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有( )
A.1个 B.2个 C.3个 D.4个
 C.
【解析】
试题分析:如图,在一个平面内,不在同一条直线上的三点,与D点恰能构成一个平行四边形,符合这样条件的点D有3个.故答案选C.
C.
【解析】
试题分析:如图,在一个平面内,不在同一条直线上的三点,与D点恰能构成一个平行四边形,符合这样条件的点D有3个.故答案选C. 下列事件:①在足球赛中,弱队战胜强队;②抛掷一枚硬币,落地后正面朝上;③任取两个正整数,其和大于1;④长度分别为3 cm,5 cm,9 cm的三条线段能围成一个三角形.其中随机事件的个数是( )
A. 1 B. 2 C. 3 D. 4
 B
【解析】①.在足球赛中,弱队可能战胜强队也可能输给强队,弱队战胜强队是随机事件。故①项符合题意。
②.抛掷1枚硬币,硬币落地时可能正面朝上也可能反面朝上,硬币落地时正面朝上是随机事件。故②项符合题意。
③.任取两个正整数,其和大于等于2,即大于1,是必然事件。故③项不符合题意。
④.由三角形的性质可知,两边之和大于第三边,3 cm+5cm<9cm,所以这三条线段不能围成...
B
【解析】①.在足球赛中,弱队可能战胜强队也可能输给强队,弱队战胜强队是随机事件。故①项符合题意。
②.抛掷1枚硬币,硬币落地时可能正面朝上也可能反面朝上,硬币落地时正面朝上是随机事件。故②项符合题意。
③.任取两个正整数,其和大于等于2,即大于1,是必然事件。故③项不符合题意。
④.由三角形的性质可知,两边之和大于第三边,3 cm+5cm<9cm,所以这三条线段不能围成... 计算
 【解析】试题分析:先乘除,后加减,按照运算顺序进行运算即可.
原式
【解析】试题分析:先乘除,后加减,按照运算顺序进行运算即可.
原式 分式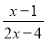 的值为零的条件是____________
的值为零的条件是____________
 【解析】试题解析::因为分式的值为0的时候,只能是分子为0,分母不能为0,所以可以得到, ;可以得到且
故答案为: .
【解析】试题解析::因为分式的值为0的时候,只能是分子为0,分母不能为0,所以可以得到, ;可以得到且
故答案为: . 小马在下面的计算题中只做对了一道题,你认为他做对的题目是( )
A. 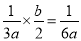 B.
B. 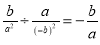
C. 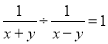 D.
D. 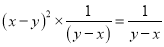
 D
【解析】试题解析:因为,所以D选项约分后等于,故答案是D选项.
故选D.
D
【解析】试题解析:因为,所以D选项约分后等于,故答案是D选项.
故选D. 计算 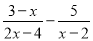 =_____________
=_____________
 【解析】试题分析:
=
=.
故答案为: .
【解析】试题分析:
=
=.
故答案为: . 如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC。
(1)求证:△AOC≌△A0E;
(2)求证:OE∥BC。
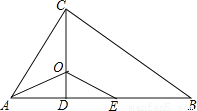
 (1)证明见解析(2)证明见解析
【解析】试题分析:
(1)由AO平分∠BAC,可得∠CAO=∠EAO结合AO=AO,AE=AC即可由“SAS”证得:△AOC≌△AOE;
(2)由△AOC≌△AOE可得∠ACO=∠AEO,由∠ACB=90°,CD⊥AB于点D,易得∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,从而可得∠DCB=∠DOE,即可得到:OE∥BC.
试题...
(1)证明见解析(2)证明见解析
【解析】试题分析:
(1)由AO平分∠BAC,可得∠CAO=∠EAO结合AO=AO,AE=AC即可由“SAS”证得:△AOC≌△AOE;
(2)由△AOC≌△AOE可得∠ACO=∠AEO,由∠ACB=90°,CD⊥AB于点D,易得∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,从而可得∠DCB=∠DOE,即可得到:OE∥BC.
试题...