题目内容
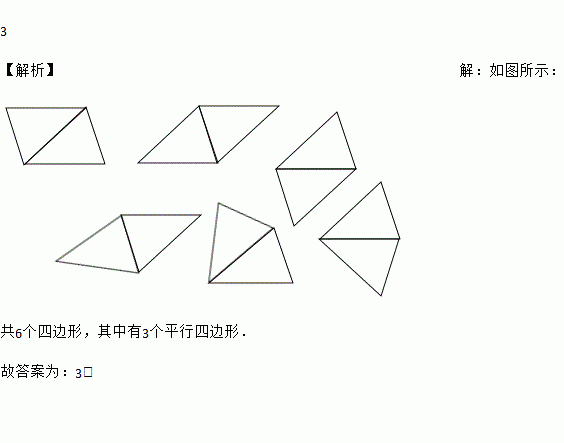
用边长为4cm，5cm，6cm的两个全等三角形一共能拼成__________个平行四边形．
3
【解析】【解析】
如图所示：
共6个四边形，其中有3个平行四边形．
故答案为：3．
练习册系列答案
天天练口算系列答案
相关题目
用适当的符号表示下列关系：
（l）a的2倍比a与3的和小； (2)y的一半与5的差是非负数；
（3）x的3倍与1的和小于x的2倍与5的差．
（1）2a＜a+3；（2）y-5≥0；（3）3x＋1＜ 2x－5
【解析】试题分析：（1）首先表示出a的2倍为2a，再表示a与3的和a+3，再利用不等式表示即可；
（2）首先表示y的一半为y，再表示与5的差为y-5，然后表示非负数即可；
（3）x的3倍与1的和表示为3x+1，x的2倍与5的差表示为2x-5，然后再抓住关键词“小于”列出不等式即可．
试题解析：（1）a的2倍为... 如图,△ABC关于直线L的轴对称图形是△DEF, 如果△ABC的面积为6CM2,且DE=3CM， 求△ABC中AB边上的高h.
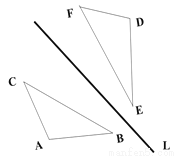
h=4cm
【解析】试题分析：本题思路的关键是利用轴对称图形的性质，得到AB =DE=3cm，然后利用面积法求出AB边上的高h.
【解析】
∵△ABC关于直线L的轴对称图形是△DEF，
∴AB =DE=3cm，
∴h=6×2÷3=4cm. 如图所示，在桌面上坚直放置两块镜面相对的平面镜，在两镜之间放一个小凳，那么在两镜中共可得到小凳的像( )
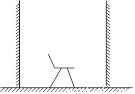
A. 2个 B. 4个 C. 16个 D. 无数个
D
【解析】∵两块镜面相对，
∴在每一块镜面中，都能有对方镜面的图像，
∴小凳在每一个镜面中都有图像.
∵每一个面中的小凳都在对面镜子中有图像，
∴循环往复，图像无数.
故选D 已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=CG，连接BG并延长交DE于F．
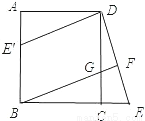
（1）求证：△BCG≌△DCE；
（2）将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形，并说明理由。
（1）答案见解析；（2）答案见解析
【解析】试题分析：（1）由正方形ABCD，得BC=CD，∠BCD=∠DCE=90°，又CG=CE，所以△BCG≌△DCE（SAS）．
（2）由（1）得BG=DE，又由旋转的性质知AE′=CE=CG，所以BE′=DG，从而证得四边形E′BGD为平行四边形．
（1）证明：∵四边形ABCD是正方形，
∴BC=CD，∠BCD=90°．
∵∠... 如图：在4×4的正方形（每个小正方形的边长均为1）网格中，以A为顶点，其他三个顶点都在格点（网格的交点）上，且面积为2的平行四边形的共有（ ）个．
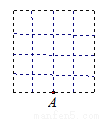
A. 10 B. 12 C. 14 D. 23
D
【解析】【解析】
一顶点在BC上，两顶点在MG上的有四边形AGIB、AOQB、AMIF、AQFO、ABMI、AFGI共6个；
一顶点在BC上，两顶点在PH上的有四边形AHVC、AVNC、APZE、AZNE、AEVN、ACZN共6个；
还有四边形AQNO、AIYL、ATXI、AHLI、APTI、AGHI、AMPI、AZRN、AVR′N、AOKN、AQSN，共11个；
... 点A、B、C是平面内不在同一条直线上的三点，点D是平面内任意一点，若A、B、C、D四点恰能构成一个平行四边形，则在平面内符合这样条件的点D有（ ）
A.1个 B.2个 C.3个 D.4个
C.
【解析】
试题分析：如图，在一个平面内，不在同一条直线上的三点，与D点恰能构成一个平行四边形，符合这样条件的点D有3个．故答案选C． 下列事件:①在足球赛中,弱队战胜强队;②抛掷一枚硬币,落地后正面朝上;③任取两个正整数,其和大于1;④长度分别为3 cm,5 cm,9 cm的三条线段能围成一个三角形.其中随机事件的个数是( )
A. 1 B. 2 C. 3 D. 4
B
【解析】①.在足球赛中，弱队可能战胜强队也可能输给强队，弱队战胜强队是随机事件。故①项符合题意。
②.抛掷1枚硬币，硬币落地时可能正面朝上也可能反面朝上，硬币落地时正面朝上是随机事件。故②项符合题意。
③.任取两个正整数，其和大于等于2，即大于1，是必然事件。故③项不符合题意。
④.由三角形的性质可知，两边之和大于第三边，3 cm+5cm<9cm，所以这三条线段不能围成... 计算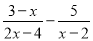 
=_____________
【解析】试题分析：
＝
＝．
故答案为： ．