题目内容
对于下列命题：（1）关于某一直线成轴对称的两个三角形全等；（2）等腰三角形的对称轴是顶角的平分线；（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点；（4）如果两个三角形全等，那么它们关于某直线成轴对称。其中真命题的个数为
A、0 B、1 C、2 D、3
C
【解析】
试题分析：根据平面图形的基本概念依次分析各小题即可作出判断.
（1）关于某一直线成轴对称的两个三角形全等，（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点，均为真命题；
（2）等腰三角形的对称轴是顶角的平分线所在的直线，（4）如果两个三角形全等，它们可能是平移或旋转构成的，均为假命题；
故选C.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知：如图，AB∥CD，求图形中的x的值．
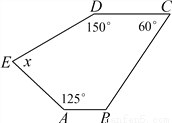
x＝85°
【解析】试题分析：先根据平行线的性质求得∠B的度数，再利用多边形的内角和定理进行求解即可.
试题解析：∵AB∥CD，∠C=60°，
∴∠B=180°-60°=120°，
∴（5-2）×180°=x+150°+125°+60°+120°，
∴x=85°． 如果a+b<0，且b>0，那么a，b，－a，－b的大小关系为（ ）.
A. a<b<－a<－b
B. －b<a<－a<b
C. a<－b<－a<b
D. a<－b<b<－a
D
【解析】∵a+b<0，且b>0，
∴a<0，|a|>b，a 若一个三角形是轴对称图形，则这个三角形一定是( ）
A. 等边三角形 B. 不等边三角形 C. 等腰三角形 D. 等腰直角三角形
C
【解析】根据轴对称图形的性质即可得出答案.
A等边三角形一定是轴对称图形，但轴对称三角形不一定是等边三角形；
B不等边三角形一定不是轴对称图形；
C等腰三角形一定是轴对称三角形；
D等腰直角三角形一定是轴对称图形，但是轴对称三角形不一定是等腰直角三角形.故选C. 如图，将一正方形纸片沿图（1）、（2）的虚线对折，得到图（3），然后沿图（3）中虚线的剪去一个角，展开得平面图形（4），则图（3）的虚线是（ ）
A．
B．
C．
D．
D
【解析】
试题分析：对于此类问题，学生只要亲自动手操作，答案就会很直观地呈现．
【解析】
由于得到的图形的中间是正方形，那么它的四分之一为等腰直角三角形．
故选D． 如图,△ABC关于直线L的轴对称图形是△DEF, 如果△ABC的面积为6CM2,且DE=3CM， 求△ABC中AB边上的高h.
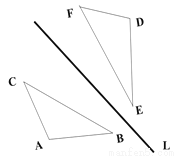
h=4cm
【解析】试题分析：本题思路的关键是利用轴对称图形的性质，得到AB =DE=3cm，然后利用面积法求出AB边上的高h.
【解析】
∵△ABC关于直线L的轴对称图形是△DEF，
∴AB =DE=3cm，
∴h=6×2÷3=4cm. 在等腰△ABC中，AB＝AC，O为不同于A的一点，且OB＝OC，则直线AO与底边BC的关系为
A、平行 B、垂直且平分 C、斜交 D、垂直不平分
B
【解析】
试题分析：先根据题意画出图形，再根据SSS证得△ABO≌△ACO，即可得到∠BAO=∠CAO，最后根据等腰三角形的三线合一的性质求解即可.
连接AO并延长
在△ABO和△ACO中，AB＝AC，OB＝OC，AO=AO
∴△ABO≌△ACO（SSS），
∴∠BAO=∠CAO，
∴AO垂直且平分BC
故选B． 已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=CG，连接BG并延长交DE于F．
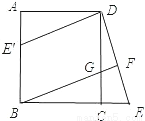
（1）求证：△BCG≌△DCE；
（2）将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形，并说明理由。
（1）答案见解析；（2）答案见解析
【解析】试题分析：（1）由正方形ABCD，得BC=CD，∠BCD=∠DCE=90°，又CG=CE，所以△BCG≌△DCE（SAS）．
（2）由（1）得BG=DE，又由旋转的性质知AE′=CE=CG，所以BE′=DG，从而证得四边形E′BGD为平行四边形．
（1）证明：∵四边形ABCD是正方形，
∴BC=CD，∠BCD=90°．
∵∠... 计算
【解析】试题分析：先乘除，后加减，按照运算顺序进行运算即可.
原式