题目内容
2.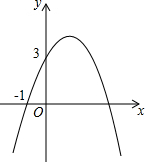 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).(1)求出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围
(3)当x取何值时,y有最大值,并求出这个最大值.
分析 (1)将(-1,0)和(0,3)两点代入二次函数y=x2+bx+c,求得b和c;从而得出抛物线的解析式;
(2)令y=0,解得x1,x2,得出此二次函数的图象与x轴的另一个交点的坐标,结合函数图象直接回答问题;
(3)根据抛物线顶点坐标回答问题.
解答 解:(1)由二次函数y=x2+bx+c的图象经过(-1,0)和(0,3)两点,
得$\left\{\begin{array}{l}{1-b+c=0}\\{c=3}\end{array}\right.$
解这个方程组,得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$
∴抛物线的解析式为y=-x2+2x+3.
(2)令y=0,得-x2+2x+3=0.
解这个方程,得x1=-1,x2=3.
因为抛物线的开口方向向下,
所以当-1<x<3时,y>0;
(3)由y=-x2+2x+3=-(x-1)2+4知,该抛物线的顶点坐标是(1,4).
故当x=1时,y最大值=4.
点评 此题考查了二次函数与x轴的交点问题以及用待定系数法求二次函数的解析式.解题时,利用了二次函数解析式的三种形式间的转化.

练习册系列答案
相关题目
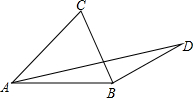 如图,在△ABC中,AB=AC=5,∠BAC=45°,将BC绕点顺时针旋转90°至BD,则AD=5$\sqrt{3}$.
如图,在△ABC中,AB=AC=5,∠BAC=45°,将BC绕点顺时针旋转90°至BD,则AD=5$\sqrt{3}$.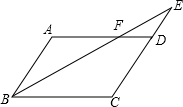 如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=CD.
如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=CD.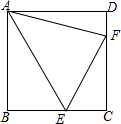 如图,正方形ABCD中,已知AB=3,点E,F分别在BC、CD上,且∠BAE=30°,∠DAF=15°,则△AEF的面积为9-3$\sqrt{3}$.
如图,正方形ABCD中,已知AB=3,点E,F分别在BC、CD上,且∠BAE=30°,∠DAF=15°,则△AEF的面积为9-3$\sqrt{3}$. 列方程解应用题:
列方程解应用题: 抛物线y=-x2-2x+49的图象如图所示.
抛物线y=-x2-2x+49的图象如图所示.