题目内容
17.方程(x-1)(x-2)(x-3)+(x-1)(x-2)(x-4)+(x-1)(x-3)(x-4)+(x-2)(x-3)(x-4)=0有( )个实根.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 把方程分成两组,分解因式得到(x-2)(x-3)(2x-5)+(x-1)(x-4)(2x-5)=0,然后提取公因式分解因式,得到2(2x-5)(x2-5x+5)=0,即可得到结论.
解答 解:(x-1)(x-2)(x-3)+(x-1)(x-2)(x-4)+(x-1)(x-3)(x-4)+(x-2)(x-3)(x-4)=0,
[(x-1)(x-2)(x-3)+(x-2)(x-3)(x-4)]+[(x-1)(x-2)(x-4)+(x-1)(x-3)(x-4)]=0,
(x-2)(x-3)(2x-5)+(x-1)(x-4)(2x-5)=0,
2(2x-5)(x2-5x+5)=0,
∴2x-5=0或x2-5x+5=0,
∵方程2x-5=0有一个解,方程x2-5x+5=0有两个解,
∴原方程有三个解,
故选D.
点评 本题考查了解一元二次方程-因式分解法,把方程分解成2(2x-5)(x2-5x+5)=0,是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.计算(3.5×103)×(2.2×105)的结果并用科学记数法表示,正确的结果是( )
| A. | 770000000 | B. | 77×107 | C. | 7.7×108 | D. | 7.7×107 |
 汽车油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数.某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图:
汽车油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数.某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图: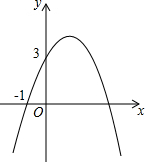 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).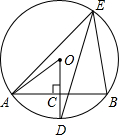 如图,AB是⊙O的一条弦,点D是弧AB的中点,OD交AB于点C,点E在⊙O上. 若∠OAC=40°,求∠DEB的度数.
如图,AB是⊙O的一条弦,点D是弧AB的中点,OD交AB于点C,点E在⊙O上. 若∠OAC=40°,求∠DEB的度数.