题目内容
13.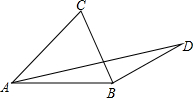 如图,在△ABC中,AB=AC=5,∠BAC=45°,将BC绕点顺时针旋转90°至BD,则AD=5$\sqrt{3}$.
如图,在△ABC中,AB=AC=5,∠BAC=45°,将BC绕点顺时针旋转90°至BD,则AD=5$\sqrt{3}$.
分析 作CM⊥AB、DN⊥AB,在Rt△ACM中,可求得AM=CM=$\frac{5\sqrt{2}}{2}$及BM的长,再证△BCM≌△DBN可得BN=CM、DN=BM,继而得AN,最后根据勾股定理即可得AD的长.
解答 解:过点C作CM⊥AB于点M,过点D作DN⊥AB,交AB延长线于点N,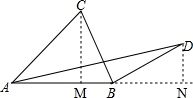
∴∠BMC=∠DNB=90°,
∵AC=5,∠CAB=45°,
∴在Rt△ACM中,AM=CM=ACsin∠CAB=$\frac{5\sqrt{2}}{2}$,
∴BM=AB-AM=5-$\frac{5\sqrt{2}}{2}$,
由旋转可知BC=BD,∠CBD=90°,
∴∠CBM+∠DBN=90°,
又∵∠CBM+∠BCM=90°,
∴∠DBN=∠BCM,
在△BCM和△DBN中,
∵$\left\{\begin{array}{l}{∠BMC=∠DNB}\\{∠BCM=∠DBN}\\{BC=BD}\end{array}\right.$,
∴△BCM≌△DBN(AAS),
∴BN=CM=$\frac{5\sqrt{2}}{2}$,DN=BM=5-$\frac{5\sqrt{2}}{2}$,
∴AN=AB+BN=5+$\frac{5\sqrt{2}}{2}$,
在Rt△ADN中,AD=$\sqrt{A{N}^{2}+D{N}^{2}}$=$\sqrt{(5+\frac{5\sqrt{2}}{2})^{2}+(5-\frac{5\sqrt{2}}{2})^{2}}$=5$\sqrt{3}$,
故答案为:5$\sqrt{3}$.
点评 本题主要考查旋转的性质及全等三角形的性质和判定、直角三角形中三角函数的应用,构建以AD为边的直角三角形是解题的关键.

练习册系列答案
相关题目
18.$\frac{3}{8}$的绝对值和相反数分别是( )
| A. | $-\frac{3}{8}$,$-\frac{3}{8}$ | B. | $\frac{3}{8}$,$\frac{3}{8}$ | C. | $-\frac{3}{8}$,$\frac{3}{8}$ | D. | $\frac{3}{8}$,$-\frac{3}{8}$ |
3. 如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
 如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°,求∠DAE的度数.
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°,求∠DAE的度数. 汽车油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数.某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图:
汽车油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数.某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图: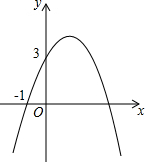 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).