题目内容
11.二次根式计算:(1)$\sqrt{9a}+\sqrt{25a}$;
(2)$\sqrt{75}-\sqrt{54}+\sqrt{96}-\sqrt{108}$;
(3)($\sqrt{48}+\frac{1}{4}\sqrt{6}$)÷$\sqrt{27}$;
(4)(2$\sqrt{3}$$+\sqrt{6}$)(2$\sqrt{3}$$-\sqrt{6}$).
分析 (1)首先化简二次根式,进而利用二次根式加减运算法则得出答案;
(2)首先化简二次根式,进而利用二次根式加减运算法则得出答案;
(3)首先化简二次根式,进而利用二次根式除法运算法则得出答案;
(4)直接利用平方差公式计算得出答案.
解答 解:(1)$\sqrt{9a}+\sqrt{25a}$=3$\sqrt{a}$+5$\sqrt{a}$=8$\sqrt{a}$;
(2)$\sqrt{75}-\sqrt{54}+\sqrt{96}-\sqrt{108}$
=5$\sqrt{3}$-3$\sqrt{6}$+4$\sqrt{6}$-6$\sqrt{3}$
=-$\sqrt{3}$+$\sqrt{6}$;
(3)($\sqrt{48}+\frac{1}{4}\sqrt{6}$)÷$\sqrt{27}$
=(4$\sqrt{3}$+$\frac{\sqrt{6}}{4}$)×$\frac{1}{3\sqrt{3}}$
=$\frac{4}{3}$+$\frac{\sqrt{2}}{12}$;
(4)(2$\sqrt{3}$$+\sqrt{6}$)(2$\sqrt{3}$$-\sqrt{6}$)
=(2$\sqrt{3}$)2-($\sqrt{6}$)2
=12-6
=6.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
19.下列各式计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C. | 2$\sqrt{3}$×$3\sqrt{3}$=6$\sqrt{3}$ | D. | $\sqrt{12}$÷$\sqrt{3}$=2 |
16.某校八年级(1)班师生从学校出发到10千米外的植物园游玩,一部分同学先步行,1小时后,其余同学骑自行车从学校出发,虽然“…”,求步行同学的速度,设步行同学的速度为xkm/h,则可列方程为$\frac{10}{x}$-$\frac{10}{3x}$=1+0.5,根据此情景和所列方程,题中“…”表示缺失的条件应该为( )
| A. | 骑自行车同学的速度比步行同学的速度多3km/h,步行的同学先到达植物园0.5h | |
| B. | 骑自行车同学的速度是步行同学的速度3倍,步行的同学先到达植物园0.5h | |
| C. | 骑自行车同学的速度是步行同学的速度3倍,骑自行车的同学先到达植物园0.5h | |
| D. | 骑自行车同学的速度比步行同学的速度多3km/h,骑自行车的同学先到达植物园0.5h |
3. 如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
 如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
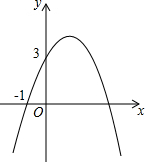 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).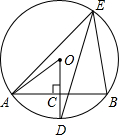 如图,AB是⊙O的一条弦,点D是弧AB的中点,OD交AB于点C,点E在⊙O上. 若∠OAC=40°,求∠DEB的度数.
如图,AB是⊙O的一条弦,点D是弧AB的中点,OD交AB于点C,点E在⊙O上. 若∠OAC=40°,求∠DEB的度数.