题目内容
7.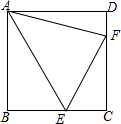 如图,正方形ABCD中,已知AB=3,点E,F分别在BC、CD上,且∠BAE=30°,∠DAF=15°,则△AEF的面积为9-3$\sqrt{3}$.
如图,正方形ABCD中,已知AB=3,点E,F分别在BC、CD上,且∠BAE=30°,∠DAF=15°,则△AEF的面积为9-3$\sqrt{3}$.
分析 如图,把△ADF绕点A逆时针旋转90°得到△ABM.则AM=AF,∠FAD=∠MAB=15°,首先证明△EAF≌EAM,推出ME=EF,推出ME=BM+BE=BE+DF,设FE=a,在Rt△ABE中,由∠ABE=90°,AB=3,∠BAE=30°,推出BE=$\sqrt{3}$,DF=a-$\sqrt{3}$,CF=3-(a-$\sqrt{3}$),根据EF2=EC2+CF2,列出方程求出a即可解决问题.
解答 解:如图,把△ADF绕点A逆时针旋转90°得到△ABM.则AM=AF,∠FAD=∠MAB=15°
∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠D=∠ABC=∠ABM=90°,
∵∠BAE=30°,∠DAF=15°,
∴∠EAF=45°,∠MAE=∠MAB+∠BAE=45°=∠EAF,
在△EAF和△EAM中,
$\left\{\begin{array}{l}{AE=AE}\\{∠EAF=∠EAM}\\{AF=AM}\end{array}\right.$,
∴△EAF≌EAM,
∴ME=EF,
∵ME=BM+BE=BE+DF,设FE=a,
在Rt△ABE中,∵∠ABE=90°,AB=3,∠BAE=30°,
∴BE=$\sqrt{3}$,DF=a-$\sqrt{3}$,CF=3-(a-$\sqrt{3}$),
∵EF2=EC2+CF2,
∴a2=(3-$\sqrt{3}$)2+[3-(a-$\sqrt{3}$)]2,
∴a=6-2$\sqrt{3}$,
∴S△AEF=S△AME=$\frac{1}{2}$•EM•AB=$\frac{1}{2}$•(6-2$\sqrt{3}$)×3=9-3$\sqrt{3}$.
故答案为9-3$\sqrt{3}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理、直角三角形30度角旋转等知识,解题的关键是灵活应用这些知识解决问题,学会添加常用辅助线的方法,记住基本图形、基本结论,属于中考常考题型.

| A. |  | B. |  | ||
| C. |  | D. |  |
| A. | $-\frac{3}{8}$,$-\frac{3}{8}$ | B. | $\frac{3}{8}$,$\frac{3}{8}$ | C. | $-\frac{3}{8}$,$\frac{3}{8}$ | D. | $\frac{3}{8}$,$-\frac{3}{8}$ |
| A. | x2-4x=3 | B. | x=0 | C. | x+2y=3 | D. | x-1=$\frac{1}{x}$ |
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C. | 2$\sqrt{3}$×$3\sqrt{3}$=6$\sqrt{3}$ | D. | $\sqrt{12}$÷$\sqrt{3}$=2 |
| A. | 骑自行车同学的速度比步行同学的速度多3km/h,步行的同学先到达植物园0.5h | |
| B. | 骑自行车同学的速度是步行同学的速度3倍,步行的同学先到达植物园0.5h | |
| C. | 骑自行车同学的速度是步行同学的速度3倍,骑自行车的同学先到达植物园0.5h | |
| D. | 骑自行车同学的速度比步行同学的速度多3km/h,骑自行车的同学先到达植物园0.5h |
| A. | -8 | B. | 8 | C. | -2 | D. | 2 |
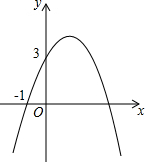 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).