题目内容
12. 抛物线y=-x2-2x+49的图象如图所示.
抛物线y=-x2-2x+49的图象如图所示.(1)若y=25时,求x的值;
(2)若y>25时,求x的取值范围.
分析 (1)把y=25代入函数关系式来求相应的x的值即可;
(2)结合函数图象可以直接得到答案.
解答 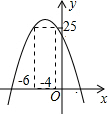 解:(1)把y=25代入,得
解:(1)把y=25代入,得
-x2-2x+49=25,
整理,得
(x+4)(x+6)=0,
解得x1=-4,x2=-6.
(2)如图所示,当y>25时,-6<x<-4.
点评 本题考查了抛物线与x轴的交点.解题时,利用了“数形结合”的数学思想.

练习册系列答案
相关题目
3. 如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
 如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
7.计算(3.5×103)×(2.2×105)的结果并用科学记数法表示,正确的结果是( )
| A. | 770000000 | B. | 77×107 | C. | 7.7×108 | D. | 7.7×107 |
17.计算(-2)÷(-$\frac{1}{2}$)×(-2)的结果是( )
| A. | -8 | B. | 8 | C. | -2 | D. | 2 |
18.若多项式x2-x-20分解为(x-a)(x-b),则a,b分别为( )
| A. | a=4,b=5 | B. | a=-4,b=5 | C. | a=4,b=-5 | D. | a=-4,b=-5 |
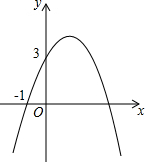 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3). 如图,六边形ABCDEF中,AF=CD,AB=DE,FE=BC,∠B=∠E,求证:AF∥CD.
如图,六边形ABCDEF中,AF=CD,AB=DE,FE=BC,∠B=∠E,求证:AF∥CD.