题目内容
12.先阅读,然后解决问题:已知:一次函数y=-x+2和反比例函数y=$\frac{-8}{x}$,求这两个函数图象在同一坐标系内的交点坐标.
解:解方程-x+2=$\frac{-8}{x}$
去分母,得
-x2+2x=-8
整理得
x2-2x-8=0
解这个方程得:x1=-2 x2=4
经检验,x1=-2 x2=4是原方程的根
当x1=-2,y1=4;x2=4,y2=-2
∴交点坐标为(-2,4)和(4,-2)
问题:
(1)在同一直角坐标系内,求反比例函数y=$\frac{4}{x}$的图象与一次函数y=x+3的图象的交点坐标;
(2)判断一次函数y=2x-3的图象与反比例函数y=-$\frac{4}{x}$的图象在同一直角坐标系内有无交点,说明理由.
分析 (1)把y=$\frac{4}{x}$的和y=x+3组成方程组,求出方程组的解即为图象在直角坐标系中的交点坐标;
(2)解方程2x-3=-$\frac{4}{x}$,整理得2x2-3x+4=0,由于△=(-3)2-4×2×4=-23<0,得到方程2x-3=-$\frac{4}{x}$无实数根,于是得到结论.
解答 解:(1)解方程x+3=$\frac{4}{x}$,
去分母,得,
x2+3x=4,
整理得,
x2+3x-4=0,
解这个方程得:x1=-1,x2=4,
经检验,x1=-1 x2=4是原方程的根,
当x1=1,y1=4;x2=-4,y2=-1,
∴交点坐标为(1,1)和(-4,-1);
(2)一次函数y=2x-3的图象与反比例函数y=-$\frac{4}{x}$的图象在同一直角坐标系内无交点,
理由:解方程2x-3=-$\frac{4}{x}$,
去分母,得
2x2-3x=-4,
整理得
2x2-3x+4=0,
∵△=(-3)2-4×2×4=-23<0,
∴方程2x-3=-$\frac{4}{x}$无实数根,
∴一次函数y=2x-3的图象与反比例函数y=-$\frac{4}{x}$的图象在同一直角坐标系内无交点.
点评 本题考查了反比例函数与一次函数的交点问题,知道方程组的解就是交点坐标是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
17.下列各图中表示数轴的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
 如图,已知线段AB=10,点C是直线AB上方一个动点,∠ACB=m°,
如图,已知线段AB=10,点C是直线AB上方一个动点,∠ACB=m°, 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°,求∠DAE的度数.
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°,求∠DAE的度数.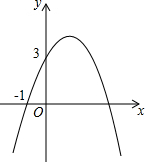 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).