题目内容
 已知如图的图形的面积为24,根据图中的条件,求出x的值.
已知如图的图形的面积为24,根据图中的条件,求出x的值.考点:一元二次方程的应用
专题:几何图形问题
分析:此图形的面积等于两个正方形的面积的差,据此可以列出方程求解.
解答:解:由题意得(x+1)2-1=24,
整理得:(x+1)2=25
即:x+1=5或 x+1=-5
∴x=4或 x=-6
∵x>0,
∴x=-6不合题意,舍去
∴x的值是4.
整理得:(x+1)2=25
即:x+1=5或 x+1=-5
∴x=4或 x=-6
∵x>0,
∴x=-6不合题意,舍去
∴x的值是4.
点评:本题考查了一元二次方程的应用,解题的关键是明确题目中的不规则图形的面积计算方法.

练习册系列答案
相关题目
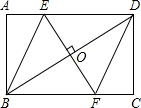 如图,矩形ABCD,过对角线BD的中点O作BD的垂线交AD于E,交BC于F,连结EB、DF.
如图,矩形ABCD,过对角线BD的中点O作BD的垂线交AD于E,交BC于F,连结EB、DF.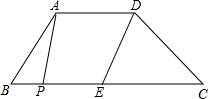 如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=4
如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=4