题目内容
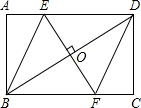 如图,矩形ABCD,过对角线BD的中点O作BD的垂线交AD于E,交BC于F,连结EB、DF.
如图,矩形ABCD,过对角线BD的中点O作BD的垂线交AD于E,交BC于F,连结EB、DF.(1)求证:四边形DEBF是菱形;
(2)若AD=3,AB=
| 3 |
考点:菱形的判定与性质,矩形的性质
专题:
分析:(1)首先证明△EDO≌△FBO,则EO=FO,根据对角线互相平分的四边形是平行四边形,证明四边形DEBF是平行四边形,然后根据对角线互相垂直的平行四边形是菱形,即可判断;
(2)设AE=x,则BE=DE=3-x,在Rt△AEB中,根据勾股定理BE2=AE2+AB2,即可列方程求解.
(2)设AE=x,则BE=DE=3-x,在Rt△AEB中,根据勾股定理BE2=AE2+AB2,即可列方程求解.
解答:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EDB=∠DBF,∠DEF=∠BFE,
在△EDO和△FBO中,
∴△EDO≌△FBO(AAS),
∴EO=FO,
∴四边形DEBF是平行四边形,
又∵DE⊥EF,
∴平行四边形DEBF是菱形;
(2)解:设AE=x,则BE=DE=3-x,而AB=
,
在Rt△AEB中,根据勾股定理BE2=AE2+AB2,
∴(3-x)2=x2+(
)2,
解得:x=1,
∴AE=1.
∴AD∥BC,
∴∠EDB=∠DBF,∠DEF=∠BFE,
在△EDO和△FBO中,
|
∴△EDO≌△FBO(AAS),
∴EO=FO,
∴四边形DEBF是平行四边形,
又∵DE⊥EF,
∴平行四边形DEBF是菱形;
(2)解:设AE=x,则BE=DE=3-x,而AB=
| 3 |
在Rt△AEB中,根据勾股定理BE2=AE2+AB2,
∴(3-x)2=x2+(
| 3 |
解得:x=1,
∴AE=1.
点评:本题考查了平行四边形的性质,以及菱形的判定方法,以及勾股定理的应用,正确掌握菱形的判定定理是关键.

练习册系列答案
相关题目
 已知如图的图形的面积为24,根据图中的条件,求出x的值.
已知如图的图形的面积为24,根据图中的条件,求出x的值.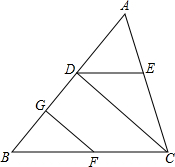 如图,已知点D、G、E、F分别是三角形ABC的边AB、AC、BC上的点,CD⊥AB于点D,∠B=∠ADE,∠EDC=∠GFB.
如图,已知点D、G、E、F分别是三角形ABC的边AB、AC、BC上的点,CD⊥AB于点D,∠B=∠ADE,∠EDC=∠GFB.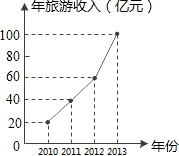 某人为了了解他所在地区的旅游情况,收集了该地区2010年至2013年每年旅游收入的有关数据,整理并绘制成折线统计图,根据图中信息,回答下列问题:
某人为了了解他所在地区的旅游情况,收集了该地区2010年至2013年每年旅游收入的有关数据,整理并绘制成折线统计图,根据图中信息,回答下列问题: