题目内容
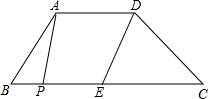 如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=4
如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=4| 2 |
(1)当x为何值时,以点P、A、D、E为顶点的四边形为直角梯形?
(2)当x为何值时,以点P、A、D、E为顶点的四边形为平行四边形?
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.
考点:直角梯形,平行四边形的判定,菱形的判定
专题:动点型
分析:(1)过D作DM⊥BC于M,求出DM、MC,根据勾股定理求出DE,推出AP⊥BC,求出即可;
(2)分为两种情况,画出图形,根据平行四边形的性质推出即可;
(3)化成图形,根据菱形的性质和判定求出BP即可.
(2)分为两种情况,画出图形,根据平行四边形的性质推出即可;
(3)化成图形,根据菱形的性质和判定求出BP即可.
解答:解:(1)过D作DM⊥BC于M,

∵CD=4
,∠C=45°,
∴DM=CM=DC×sin45°=4
×
=4,
∵E是BC的中点,BC=12,
∴BE=CE=6,
∴EM=6-4=2,
在Rt△DME中,由勾股定理得:DE=
=2
,
∵要使以点P、A、D、E为顶点的四边形为直角梯形,
∴只能是∠APB=90°,
即AP⊥BC,AP⊥AD,如图2,
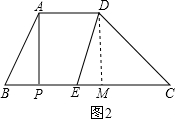
∵AP=DM,AP∥DM,
∴四边形APMD是矩形,
∴AD=PM=5,
∴PE=5-2=3,
∴BP=12-6-3=3,
即当x为3时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)分为两种情况:①如图3,当P在E的左边时,
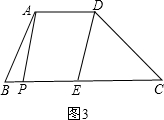
∵AD=PE=5,CE=6,
∴BP=12-6-5=1;
②如图4,当P在E的右边时,
∵AD=EP=5,
∴BP=12-(6-5)=11;
即当x为1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能构成菱形,
理由是:分为两种情况:①当P在E的左边时,如图3,
∵AD=5,DE=2
,
∴AD≠DE,
即此时以点P、A、D、E为顶点的四边形APED不是菱形;
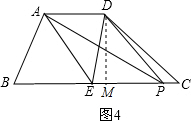
②如图4,过点D作DM⊥BC于点M,当P在E的右边时,过A作AQ⊥BC于Q,
则AQ=DM=4,
∵AD=AE=EP=5,
∴BP=BP=6+5=11;
即当x为11时,以点P、A、D、E为顶点的四边形为菱形.

∵CD=4
| 2 |
∴DM=CM=DC×sin45°=4
| 2 |
| ||
| 2 |
∵E是BC的中点,BC=12,
∴BE=CE=6,
∴EM=6-4=2,
在Rt△DME中,由勾股定理得:DE=
| 42+22 |
| 5 |
∵要使以点P、A、D、E为顶点的四边形为直角梯形,
∴只能是∠APB=90°,
即AP⊥BC,AP⊥AD,如图2,

∵AP=DM,AP∥DM,
∴四边形APMD是矩形,
∴AD=PM=5,
∴PE=5-2=3,
∴BP=12-6-3=3,
即当x为3时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)分为两种情况:①如图3,当P在E的左边时,

∵AD=PE=5,CE=6,
∴BP=12-6-5=1;
②如图4,当P在E的右边时,
∵AD=EP=5,
∴BP=12-(6-5)=11;
即当x为1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能构成菱形,
理由是:分为两种情况:①当P在E的左边时,如图3,
∵AD=5,DE=2
| 5 |
∴AD≠DE,
即此时以点P、A、D、E为顶点的四边形APED不是菱形;

②如图4,过点D作DM⊥BC于点M,当P在E的右边时,过A作AQ⊥BC于Q,
则AQ=DM=4,
∵AD=AE=EP=5,
∴BP=BP=6+5=11;
即当x为11时,以点P、A、D、E为顶点的四边形为菱形.
点评:本题考查了平行四边形的判定和性质,菱形的判定,直角梯形的判定,勾股定理等知识点的应用,用了分类讨论思想,题目比较好,但是比较容易出错.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
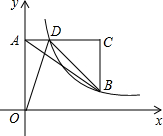 如图,在平面直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B、C的横坐标都是3,且BC=2,点D在AC上,若反比例函数y=
如图,在平面直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B、C的横坐标都是3,且BC=2,点D在AC上,若反比例函数y= 已知如图的图形的面积为24,根据图中的条件,求出x的值.
已知如图的图形的面积为24,根据图中的条件,求出x的值.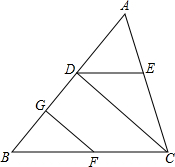 如图,已知点D、G、E、F分别是三角形ABC的边AB、AC、BC上的点,CD⊥AB于点D,∠B=∠ADE,∠EDC=∠GFB.
如图,已知点D、G、E、F分别是三角形ABC的边AB、AC、BC上的点,CD⊥AB于点D,∠B=∠ADE,∠EDC=∠GFB.
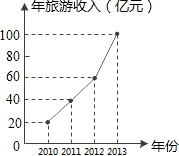 某人为了了解他所在地区的旅游情况,收集了该地区2010年至2013年每年旅游收入的有关数据,整理并绘制成折线统计图,根据图中信息,回答下列问题:
某人为了了解他所在地区的旅游情况,收集了该地区2010年至2013年每年旅游收入的有关数据,整理并绘制成折线统计图,根据图中信息,回答下列问题: