题目内容
(1)设a-b=4,a2+b2=10,求(a+b)2的值;
(2)观察下列式子:1×3+1=4,2×4+1=9,3×5+1=16,4×6+1=25,…,探索以上式子的规律,试写出第n个等式,并说明第n个等式成立.
(2)观察下列式子:1×3+1=4,2×4+1=9,3×5+1=16,4×6+1=25,…,探索以上式子的规律,试写出第n个等式,并说明第n个等式成立.
考点:完全平方公式,规律型:数字的变化类
专题:计算题
分析:(1)将a-b=4两边平方,利用完全平方公式展开,把a2+b2=10代入计算求出2ab的值,原式利用完全平方公式展开后,把各自的值代入计算即可求出值;
(2)观察一系列等式,得到一般性规律,验证即可.
(2)观察一系列等式,得到一般性规律,验证即可.
解答:解:(1)∵a-b=4,a2+b2=10,
∴(a-b)2=a2+b2-2ab,即16=10-2ab,
整理得:2ab=-6,
则(a+b)2=a2+b2+2ab=10-6=4;
(2)观察已知,归纳总结得:n(n+2)+1=(n+1)2,
验证:左边=n2+2n+1=(n+1)2=右边.
∴(a-b)2=a2+b2-2ab,即16=10-2ab,
整理得:2ab=-6,
则(a+b)2=a2+b2+2ab=10-6=4;
(2)观察已知,归纳总结得:n(n+2)+1=(n+1)2,
验证:左边=n2+2n+1=(n+1)2=右边.
点评:此题考查了完全平方公式,熟练掌握公式是解本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,已知△ABC中,DE∥BC,将△ADE沿DE翻折,使得点A落在平面内的A′处,若
如图,已知△ABC中,DE∥BC,将△ADE沿DE翻折,使得点A落在平面内的A′处,若∠B=50°,则∠BDA′的度数是( )
| A、90° | B、100° |
| C、80° | D、70° |
某项工作,甲单独做要4天完成,乙单独做要6天完成,若甲先做1天后,然后甲、乙合作完成此项工作,若设甲一共做了x天,所列方程是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知点M(2,3)在双曲线y=
上,则下列各点一定不在该双曲线上的是( )
| k |
| x |
| A、(3,2) |
| B、(-2,-3) |
| C、(1,6) |
| D、(3,-2) |
 如图,在平行四边形ABCD中,AC=12cm,BD=6cm,求AD的长和四边形的面积.
如图,在平行四边形ABCD中,AC=12cm,BD=6cm,求AD的长和四边形的面积.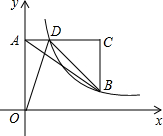 如图,在平面直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B、C的横坐标都是3,且BC=2,点D在AC上,若反比例函数y=
如图,在平面直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B、C的横坐标都是3,且BC=2,点D在AC上,若反比例函数y= 已知如图的图形的面积为24,根据图中的条件,求出x的值.
已知如图的图形的面积为24,根据图中的条件,求出x的值.