题目内容
先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式x2-4>0
解:∵x2-4=(x+2)(x-2)
∴x2-4>0可化为 (x+2)(x-2)>0
①
由有理数的乘法法则“两数相乘,同号得正”,得②
或
解不等式组①,得x>2;解不等式组②,得x<-2,
∴(x+2)(x-2)>0的解集为x>2或x<-2,即一元二次不等式x2-4>0的解集为x>2或x<-2.
根据阅读材料:
(1)一元二次不等式x2-16>0的解集为 (在横线上直接写出答案);
(2)解不等式
>0;
(3)解不等式
>1.
例题:解一元二次不等式x2-4>0
解:∵x2-4=(x+2)(x-2)
∴x2-4>0可化为 (x+2)(x-2)>0
①
|
|
解不等式组①,得x>2;解不等式组②,得x<-2,
∴(x+2)(x-2)>0的解集为x>2或x<-2,即一元二次不等式x2-4>0的解集为x>2或x<-2.
根据阅读材料:
(1)一元二次不等式x2-16>0的解集为
(2)解不等式
| x-1 |
| x-3 |
(3)解不等式
| x |
| 2x-1 |
考点:一元一次不等式组的应用
专题:阅读型
分析:(1)将一元二次不等式的左边因式分解后化为两个一元一次不等式组求解即可;
(2)根据分式不等式大于零可以得到其分子、分母同号,从而转化为两个一元一次不等式组求解即可;
(3)将不等式
>1进行变形,得出
>0,然后转化成两个一元一次不等式组,最后求解即可;
(2)根据分式不等式大于零可以得到其分子、分母同号,从而转化为两个一元一次不等式组求解即可;
(3)将不等式
| x |
| 2x-1 |
| 1-x |
| 2x-1 |
解答:解:(1)∵x2-16=(x+4)(x-4),
∴x2-16>0可化为 (x+4)(x-4)>0
由有理数的乘法法则“两数相乘,同号得正”,得
,
解第一个不等式组,得x>4,
解第二个不等式组,得x<-4,
∴(x+4)(x-4)>0的解集为x>4或x<-4,
即一元二次不等式x2-16>0的解集为x>4或x<-4.
(2)∵
>0,
∴
或
,
解得:x>3或x<1;
(3)∵
>1,
∴
>0,
∴
或
,
解得:解第一个不等式组,得
<x<1;
解第二个不等式组得,不等式组无解,
∴不等式组的解集是
<x<1.
∴x2-16>0可化为 (x+4)(x-4)>0
由有理数的乘法法则“两数相乘,同号得正”,得
|
|
解第一个不等式组,得x>4,
解第二个不等式组,得x<-4,
∴(x+4)(x-4)>0的解集为x>4或x<-4,
即一元二次不等式x2-16>0的解集为x>4或x<-4.
(2)∵
| x-1 |
| x-3 |
∴
|
|
解得:x>3或x<1;
(3)∵
| x |
| 2x-1 |
∴
| 1-x |
| 2x-1 |
∴
|
|
解得:解第一个不等式组,得
| 1 |
| 2 |
解第二个不等式组得,不等式组无解,
∴不等式组的解集是
| 1 |
| 2 |
点评:此题考查了不等式组的解法,利用了转化的思想,这种转化思想的依据为:两数相乘(除),同号得正,异号得负的取符号法则.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在平行四边形ABCD中,AC=12cm,BD=6cm,求AD的长和四边形的面积.
如图,在平行四边形ABCD中,AC=12cm,BD=6cm,求AD的长和四边形的面积. 已知如图的图形的面积为24,根据图中的条件,求出x的值.
已知如图的图形的面积为24,根据图中的条件,求出x的值.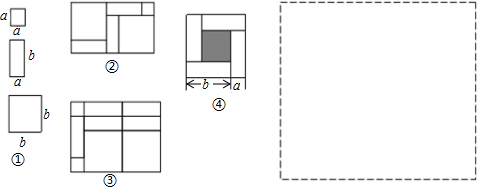
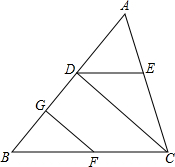 如图,已知点D、G、E、F分别是三角形ABC的边AB、AC、BC上的点,CD⊥AB于点D,∠B=∠ADE,∠EDC=∠GFB.
如图,已知点D、G、E、F分别是三角形ABC的边AB、AC、BC上的点,CD⊥AB于点D,∠B=∠ADE,∠EDC=∠GFB.