题目内容
15. 如图,在?ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为4cm.
如图,在?ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为4cm.
分析 由平行四边形的性质得出BC=AD=12cm,AD∥BC,得出∠DAE=∠BEA,证出∠BEA=∠BAE,得出BE=AB,即可得出CE的长.
解答 解:∵四边形ABCD是平行四边形,
∴BC=AD=12cm,AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BEA=∠BAE,
∴BE=AB=8cm,
∴CE=BC-BE=4cm.
故答案为:4cm.
点评 本题考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,证出BE=AB是解决问题的关键.

练习册系列答案
相关题目
3.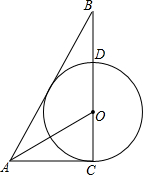 如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )
 如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )| A. | π | B. | 2π | C. | $\frac{9}{4}$π | D. | $\frac{16}{9}$π |
4.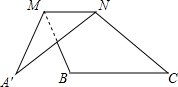 如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )
如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )
 如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )
如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )| A. | 88° | B. | 116° | C. | 126° | D. | 112° |
 如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.求证:∠AMD=∠AGF.
如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.求证:∠AMD=∠AGF.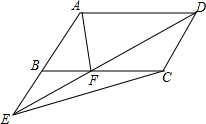 如图所示,E是?ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF=S△EFC.
如图所示,E是?ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF=S△EFC.