题目内容
19.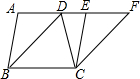 如图,在四边形ABCD中,AD∥BC,且AD<BC,连接BD,现将三角形ABD平移到三角形ECF的位置.
如图,在四边形ABCD中,AD∥BC,且AD<BC,连接BD,现将三角形ABD平移到三角形ECF的位置.(1)指出平移的方向和平移的距离;
(2)求证:AF=AD+BC;
(3)若AD=$\frac{2}{3}$BC,三角形ABD的面积为15,求四边形ABCF的面积.
分析 (1)找到一对对应点,那么从△ABD的对应点到△ECF对应点即为平移的方向,对应点的连线即为平移的距离;
(2)根据平移的性质易得BC=DF,根据AF由AD和DF组成可得AD+BC=AF;
(3)根据平移的性质易得DF=BC,进而由AD=$\frac{2}{3}$BC得出三角形BDC的面积为$\frac{45}{2}$,S梯形ABFD=15+$2×\frac{45}{2}$,即可求出.
解答 解:(1)平移的方向是点B到点C的方向,平移的距离是线段BC的长度;
(2)∵△ABD平移到△ECF的位置,
∴DF=BC,
∵AD+DF=AF,
∴AD+BC=AF.
(3)∵AD=$\frac{2}{3}$BC,三角形ABD的面积为15,
∴三角形BDC的面积为$\frac{45}{2}$,
∵DF=BC,
∴三角形DCF的面积为$\frac{45}{2}$,
∴S梯形ABFD=15+$2×\frac{45}{2}$=60.
点评 本题考查平移的知识,用到的知识点为:图形平移前后对应线段平行且相等;对应点的连线为两个图形平移的距离.

练习册系列答案
相关题目
10.下列关于x的方程中,无理方程是( )
| A. | ${x^2}+\sqrt{5}x+1=0$ | B. | $\sqrt{2}x+1=0$ | C. | $\sqrt{x+1}+\sqrt{2}=0$ | D. | $\sqrt{a-1}$+2x=7 |
14.下列计算正确的是( )
| A. | 3$\sqrt{3}-\sqrt{3}$=3 | B. | 2$\sqrt{3}+3\sqrt{3}=5\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{5}+\frac{3\sqrt{2}}{5}=\sqrt{5}$ | D. | 3$\sqrt{6}-6\sqrt{6}=3\sqrt{6}$ |
4.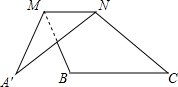 如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )
如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )
 如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )
如图,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A=28°,∠B=120°,则∠A′NC多少度?( )| A. | 88° | B. | 116° | C. | 126° | D. | 112° |
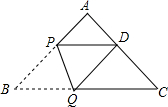 如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D (不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为2或2$\sqrt{2}$-2.
如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D (不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为2或2$\sqrt{2}$-2.