题目内容
18.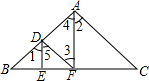 如图所示,点D,A在直线AB上,点E,F在直线BC上,连接AC、DE、DF、AF.
如图所示,点D,A在直线AB上,点E,F在直线BC上,连接AC、DE、DF、AF.(1)∠1、∠4是直线DE与AF被直线AB所截得的同位角角,∠2、∠3是直线DF与AC被直线AF所截得的内错角.
(2)若∠1=∠5,∠2=∠4,∠1=∠2,找出图中的两组平行线,并说明理由.
分析 (1)同位角就是:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角,内错角是两个角在两直线的中间,截线的两侧,可得答案;
(2)根据平行线的判定,可得答案.
解答 解:(1)∠1、∠4是直线 DE与AF被直线 AB所截得的 同位角角,∠2、∠3是直线 DF与AC被直线 AF所截得的 内错角,
故答案为:DE与AF,AB,同位角,DF与AC,AF,内错;
(2)DE∥AF,理由如下:
∵∠1=∠2,∠2=∠4,
∴∠1=∠4,
∴DE∥AF;
DF∥AC,理由如下:
∵DE∥AF,
∴∠5=∠3.
∵∠5=∠1=∠3,∠1=∠4=∠2,
∴∠3=∠2,
∴DF∥AC.
点评 本题考查了同位角、内错角、同旁内角,熟记三线八角的定义是解题关键,利用了平行线的判定.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
9.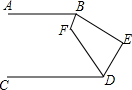 如图,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠F=125°,则∠E的度数为( )
如图,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠F=125°,则∠E的度数为( )
 如图,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠F=125°,则∠E的度数为( )
如图,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠F=125°,则∠E的度数为( )| A. | 120° | B. | 115° | C. | 110° | D. | 105° |
3.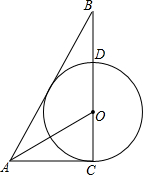 如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )
 如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )| A. | π | B. | 2π | C. | $\frac{9}{4}$π | D. | $\frac{16}{9}$π |
 如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.求证:∠AMD=∠AGF.
如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.求证:∠AMD=∠AGF.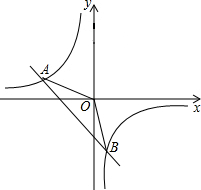 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)