题目内容
1.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D,C分别在M,N的位置上,若∠EFG=56°,则∠1=68°,∠2=112°.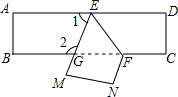
分析 首先根据折叠的性质和平行线的性质求∠FED的度数,然后根据三角形内角和定理求出∠1的度数,最后根据平行线的性质求出∠2的度数.
解答 解:∵一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D,C分别在M,N的位置上,
∴∠MEF=∠FED,∠EFC+∠GFE=180°,
∵AD∥BC,∠EFG=56°,
∴∠FED=∠EFG=56°,
∵∠1+∠GEF+∠FED=180°,
∴∠1=180°-56°-56°=68°,
又∵∠1+∠2=180°,
∴∠2=180°-68°=112°.
故答案为:68°,112°.
点评 本题考查了平行线的性质,翻折变换的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
9.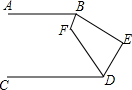 如图,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠F=125°,则∠E的度数为( )
如图,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠F=125°,则∠E的度数为( )
 如图,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠F=125°,则∠E的度数为( )
如图,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠F=125°,则∠E的度数为( )| A. | 120° | B. | 115° | C. | 110° | D. | 105° |
10.下列关于x的方程中,无理方程是( )
| A. | ${x^2}+\sqrt{5}x+1=0$ | B. | $\sqrt{2}x+1=0$ | C. | $\sqrt{x+1}+\sqrt{2}=0$ | D. | $\sqrt{a-1}$+2x=7 |

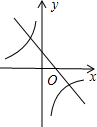
 如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.求证:∠AMD=∠AGF.
如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.求证:∠AMD=∠AGF.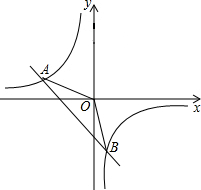 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)