题目内容
10.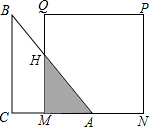 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一条直线上,开始时点A与点N重合,让△ABC以2cm/s的速度向左运动,最终点A与点M重合.求:
如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一条直线上,开始时点A与点N重合,让△ABC以2cm/s的速度向左运动,最终点A与点M重合.求:(1)重叠部分的面积y(cm2)与时间t(s)之间的函数表达式和自变量的取值范围;
(2)当t=1,t=2时,求重叠部分的面积.
分析 (1)由题意可知:重叠部分也是等腰直角三角形,又因为AN=2t,所以AM=MN-AN=20-2t,MH=AM=20-2t,利用三角形面积公式即可表示出重叠部分的面积.
(2)分别令t=1和t=2代入(1)中的函数表达式即可求出答案.
解答 解:(1)∵△ABC是等腰直角三角形,
∴重叠部分也是等腰直角三角形.
又∵AN=2t,∴AM=MN-AN=20-2t,
∴MH=AM=20-2t,
∴重叠部分的面积为y=$\frac{1}{2}$(20-2t)2=2t2-40t+200.
自变量的取值范围是0≤t≤10;
(2)当t=1时,y=162(cm2),
当t=2时,y=128(cm2).
点评 本题考查二次函数的应用,涉及代入求值问题,等腰三角形性质与判定,三角形面积公式等知识.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
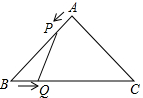 如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t s,四边形APQC的面积为y cm2.
如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t s,四边形APQC的面积为y cm2.