题目内容
4.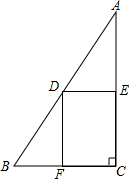 如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=12,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.(1)求y关于x的函数关系式,并求出x的取值范围;
(2)设四边形DECF的面积为S,求S与x之间的函数关系式,并求出当x为何值时,S有最大值?最大值是多少?
分析 (1)根据余角的性质即可推出∠A=∠BDF,继而求证△ADE∽△DBF,结合对应边成比例和BF=6-x,AE=12-y,即可求出y=-2x+12(0<x<6);
(2)根据(1)所推出的结论,结合矩形的面积公式通过等量代换,即可求出二次函数S=DE•DF=-2x2+12x,然后根据二次函数的最值公式即可求出S的最大值.
解答 解:(1)∵∠C=90°,DE⊥AC,DF⊥BC,
∴∠A+∠B=90°,∠BDF+∠ADE=90°,
∴∠A=∠BDF,
∴△ADE∽△DBF,
∴$\frac{AE}{DF}$=$\frac{DE}{BF}$,
∵四边形DECF是矩形,DF=y,DE=x,
∴CF=x,CE=y,
∴BF=BC-CF=6-x,
∵AE=12-y,
∴$\frac{12-y}{y}$=$\frac{x}{6-x}$,
∴y=-2x+12(0<x<6),
(4)∵y=-2x+12,DE=x,DF=y,
∴S=DE•DF=xy=x(-2x+12)=-2x2+12x=-2(x2-6x+9)+18,
即S=-2(x-3)2+18,
∴当x=3时,S有最大值,最大值是18.
点评 本题主要考查相似三角形的判定与性质,矩形的判定与性质,矩形的面积,二次函数的最值等知识点,角的三角函数,关键在于求证△ADE∽△DBF,用关于x、y的式子表达出相关的线段,认真地进行计算.

练习册系列答案
相关题目
16.使一次函数y=(m+2)x+m-2不经过第二象限,且使关于x的不等式组$\left\{\begin{array}{l}{x>m-2}\\{-3x+2≥6m-1}\end{array}\right.$有解的所有整数m的和为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
 已知平面直角坐标系中,点A(-3,3)、B(-2,-2).
已知平面直角坐标系中,点A(-3,3)、B(-2,-2).
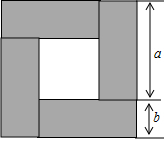 把四块长为a,宽为b的长方形木板围成如图所示的正方形,请解答下列问题:
把四块长为a,宽为b的长方形木板围成如图所示的正方形,请解答下列问题:
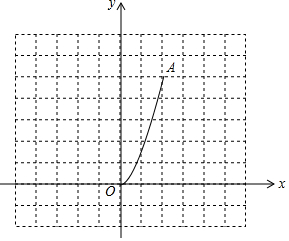 如图,二次函数y=$\frac{5}{4}$x2(0≤x≤2)的图象记为曲线C1,将C1绕坐标原点O逆时针旋转90°,得曲线C2.
如图,二次函数y=$\frac{5}{4}$x2(0≤x≤2)的图象记为曲线C1,将C1绕坐标原点O逆时针旋转90°,得曲线C2.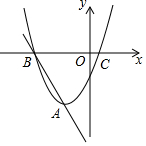 已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.
已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.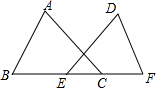 如图,点E,C在BF上,BE=CF,AB=DF,∠B=∠F.求证:∠A=∠D.
如图,点E,C在BF上,BE=CF,AB=DF,∠B=∠F.求证:∠A=∠D.