题目内容
20.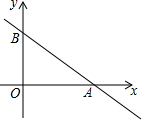 如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
分析 分两种情形:①当AB∥CD时,CD=AB=10,②当CD为对角线时,AB的中点E(4,3),设C(x,-x),求出CE,构建二次函数利用二次函数的性质解决最值问题.
解答 解:①当AB∥CD时,CD=AB=10,
②当CD为对角线时,AB的中点E(4,3),设C(x,-x),
CE=$\sqrt{(x-4)^{2}+(-x-3)^{2}}$=$\sqrt{2{x}^{2}-2x+25}$=$\sqrt{2(x-\frac{1}{2})^{2}+\frac{49}{2}}$,
当x=$\frac{1}{2}$时,CE最小=$\frac{7\sqrt{2}}{2}$,
此时CD最小=7$\sqrt{2}$.
∵7$\sqrt{2}$<10,
∴CD的最小值为7$\sqrt{2}$.
故答案为7$\sqrt{2}$.
点评 本题考查平行四边形的性质、一次函数、两点之间的距离公式等知识,解题的关键是学会分类讨论,构建二次函数利用二次函数的性质解决最值问题,属于中考常考题型.

练习册系列答案
相关题目
8.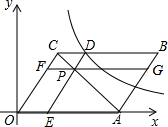 如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数$y=\frac{k}{x}$的图象经过点D,四边形BCFG的面积为8,则k的值为( )
如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数$y=\frac{k}{x}$的图象经过点D,四边形BCFG的面积为8,则k的值为( )
 如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数$y=\frac{k}{x}$的图象经过点D,四边形BCFG的面积为8,则k的值为( )
如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数$y=\frac{k}{x}$的图象经过点D,四边形BCFG的面积为8,则k的值为( )| A. | 16 | B. | 20 | C. | 24 | D. | 28 |
12.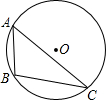 如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则$\widehat{BC}$的长为( )
如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则$\widehat{BC}$的长为( )
 如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则$\widehat{BC}$的长为( )
如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则$\widehat{BC}$的长为( )| A. | 2π | B. | 4π | C. | 6π | D. | 12π |
10.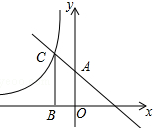 如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )
如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )
 如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )
如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )| A. | y=$\frac{3}{x}$ | B. | y=-$\frac{3}{x}$ | C. | y=$\frac{3}{2x}$ | D. | y=-$\frac{3}{2x}$ |

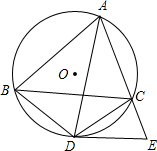 如图,锐角△ABC内接于⊙O,点D是弧BC上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC,连接AD、BD、CD.
如图,锐角△ABC内接于⊙O,点D是弧BC上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC,连接AD、BD、CD. 如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧,$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述做法得到的曲线AA1A2A3A4A5…称为正方形的渐开线“,那么点A5的坐标是(6,0),点A2016的坐标是(1,2017).
如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧,$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述做法得到的曲线AA1A2A3A4A5…称为正方形的渐开线“,那么点A5的坐标是(6,0),点A2016的坐标是(1,2017).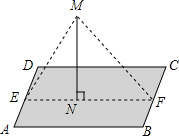 “五一期间”某公司在一块平行四边形ABCD的湖中,立有一个旗杆MN,MN与湖面垂直,旗杆顶端M与湖岸的E、F两处用绳子相连.绳子上系满了彩旗.且直线EF经过旗杆底部N,EF∥AB,已知,AB=40($\sqrt{3}$+1)m.BC=30m.∠MEN=60°,∠MFN=45°,求绳子EM的长.
“五一期间”某公司在一块平行四边形ABCD的湖中,立有一个旗杆MN,MN与湖面垂直,旗杆顶端M与湖岸的E、F两处用绳子相连.绳子上系满了彩旗.且直线EF经过旗杆底部N,EF∥AB,已知,AB=40($\sqrt{3}$+1)m.BC=30m.∠MEN=60°,∠MFN=45°,求绳子EM的长.