题目内容
5.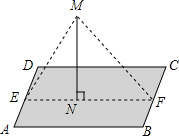 “五一期间”某公司在一块平行四边形ABCD的湖中,立有一个旗杆MN,MN与湖面垂直,旗杆顶端M与湖岸的E、F两处用绳子相连.绳子上系满了彩旗.且直线EF经过旗杆底部N,EF∥AB,已知,AB=40($\sqrt{3}$+1)m.BC=30m.∠MEN=60°,∠MFN=45°,求绳子EM的长.
“五一期间”某公司在一块平行四边形ABCD的湖中,立有一个旗杆MN,MN与湖面垂直,旗杆顶端M与湖岸的E、F两处用绳子相连.绳子上系满了彩旗.且直线EF经过旗杆底部N,EF∥AB,已知,AB=40($\sqrt{3}$+1)m.BC=30m.∠MEN=60°,∠MFN=45°,求绳子EM的长.
分析 由平行四边形的判定与性质得到EF=AB,在直角△MNF和直角△MEN中利用勾股定理来求EM的长度.
解答 解:设EN=x,
∵∠MEN=60°,∠ENM=90°,
∴EM=2x,MN=$\sqrt{3}$x,
∵∠MFN=45°,
∴MN=NF=$\sqrt{3}$x,
由题意可得:AB=EF=EN+NF=x+$\sqrt{3}$x=40($\sqrt{3}$+1),
解得:x=40,
则EN=80(m).
答:绳子EM的长为80m.
点评 此题主要考查了平行四边形的性质以及锐角三角函数关系,得出EN的值是解题关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
20.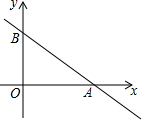 如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
 如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
10.清明节是中国传统节日,它不仅是人们远足踏青的日子,更是祭奠祖先、缅怀先人的节日.市民政局提供的数据显示,今年清明节当天全市213处祭扫点共接待群众264000人,将264000用科学记数法表示应为( )
| A. | 264×103 | B. | 2.64×104 | C. | 2.64×105 | D. | 0.264×106 |
 如图,△ABC内接于⊙O,若∠BAC=30°,BC=2,则⊙O的半径为2.
如图,△ABC内接于⊙O,若∠BAC=30°,BC=2,则⊙O的半径为2.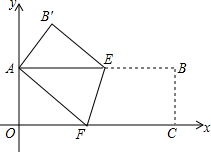 如图,矩形纸片AOCB,以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,折叠纸片,使点C与点A重合,点B落在点B′处,折痕为EF,若顶点B的坐标为(9,3),求点E、F、B′的坐标.
如图,矩形纸片AOCB,以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,折叠纸片,使点C与点A重合,点B落在点B′处,折痕为EF,若顶点B的坐标为(9,3),求点E、F、B′的坐标. 如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2017秒时,点P的坐标是(2017,1).
如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2017秒时,点P的坐标是(2017,1).