题目内容
10.在如图平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是($\frac{\sqrt{3}}{3}$)2014.
分析 利用正方形的性质结合锐角三角函数关系得出正方形的边长,进而得出变化规律即可得出答案.
解答 解:如图所示:∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…
∴D1E1=B2E2,D2E3=B3E4,∠D1C1E1=∠C2B2E2=∠C3B3E4=30°,
∴D1E1=C1D1sin30°=$\frac{1}{2}$,则B2C2=($\frac{\sqrt{3}}{3}$)1,
同理可得:B3C3=$\frac{1}{3}$=($\frac{\sqrt{3}}{3}$)2,
故正方形AnBnCnDn的边长是:($\frac{\sqrt{3}}{3}$)n-1.
则正方形A2015B2015C2015D2015的边长是:($\frac{\sqrt{3}}{3}$)2014.
故答案是:($\frac{\sqrt{3}}{3}$)2014.
点评 此题主要考查了正方形的性质以及锐角三角函数关系,得出正方形的边长变化规律是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.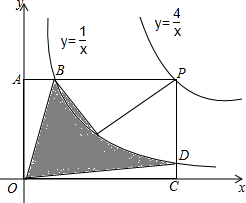 如图,点P为反比例函数y=$\frac{4}{x}$(x>0)图象上一点,过点P作y轴的垂线,交双曲线y=$\frac{1}{x}$于点B,交y轴于点A,过点P作x轴的垂线,交双曲线y=$\frac{1}{x}$于点D,交x轴于点C,连接OP交双曲线y=$\frac{1}{x}$于点E,则连接BO,OD,DE,EB而围成的阴影部分面积为( )
如图,点P为反比例函数y=$\frac{4}{x}$(x>0)图象上一点,过点P作y轴的垂线,交双曲线y=$\frac{1}{x}$于点B,交y轴于点A,过点P作x轴的垂线,交双曲线y=$\frac{1}{x}$于点D,交x轴于点C,连接OP交双曲线y=$\frac{1}{x}$于点E,则连接BO,OD,DE,EB而围成的阴影部分面积为( )
 如图,点P为反比例函数y=$\frac{4}{x}$(x>0)图象上一点,过点P作y轴的垂线,交双曲线y=$\frac{1}{x}$于点B,交y轴于点A,过点P作x轴的垂线,交双曲线y=$\frac{1}{x}$于点D,交x轴于点C,连接OP交双曲线y=$\frac{1}{x}$于点E,则连接BO,OD,DE,EB而围成的阴影部分面积为( )
如图,点P为反比例函数y=$\frac{4}{x}$(x>0)图象上一点,过点P作y轴的垂线,交双曲线y=$\frac{1}{x}$于点B,交y轴于点A,过点P作x轴的垂线,交双曲线y=$\frac{1}{x}$于点D,交x轴于点C,连接OP交双曲线y=$\frac{1}{x}$于点E,则连接BO,OD,DE,EB而围成的阴影部分面积为( )| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
2. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )
 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )| A. | 5×($\frac{3}{2}$)2016 | B. | 5×($\frac{9}{4}$)2016 | C. | 5×($\frac{9}{4}$)2015 | D. | 5×($\frac{3}{2}$)4032 |
19.已知菱形ABCD的一边为10cm,则它的周长是( )
| A. | 10cm | B. | 20cm | C. | 30cm | D. | 40cm |
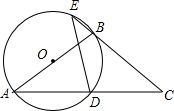 如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.
如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.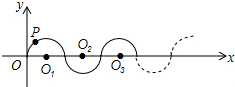 如图,在平面直角坐标系中,半径均为1各单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是(2015,-1).
如图,在平面直角坐标系中,半径均为1各单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是(2015,-1). 如图,△ABC内接于⊙O,若∠BAC=30°,BC=2,则⊙O的半径为2.
如图,△ABC内接于⊙O,若∠BAC=30°,BC=2,则⊙O的半径为2.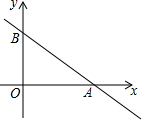 如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.