题目内容
11.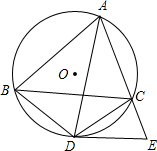 如图,锐角△ABC内接于⊙O,点D是弧BC上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC,连接AD、BD、CD.
如图,锐角△ABC内接于⊙O,点D是弧BC上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC,连接AD、BD、CD.求证:△ABD∽△ADE.
分析 由平行线得出$\widehat{BD}=\widehat{CD}$,∠ACB=∠AED,得出∠BAD=∠DAC,由圆周角定理得出∠ACB=∠ADB,证出∠ADB=∠AED,即可得出结论.
解答 证明:∵DE∥BC,
∴$\widehat{BD}=\widehat{CD}$,∠ACB=∠AED,
∴∠BAD=∠DAC,
∵∠ACB=∠ADB,
∴∠ADB=∠AED,
∴△ABD∽△ADE.
点评 本题考查了相似三角形的判定、圆周角定理、平行线的性质;熟练掌握相似三角形的判定方法,由平行线和圆周角定理得出相等的角是解决问题的关键.

练习册系列答案
相关题目
2. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )
 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )| A. | 5×($\frac{3}{2}$)2016 | B. | 5×($\frac{9}{4}$)2016 | C. | 5×($\frac{9}{4}$)2015 | D. | 5×($\frac{3}{2}$)4032 |
19.已知菱形ABCD的一边为10cm,则它的周长是( )
| A. | 10cm | B. | 20cm | C. | 30cm | D. | 40cm |
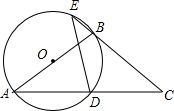 如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.
如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.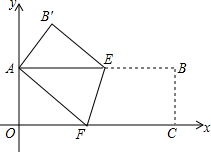 如图,矩形纸片AOCB,以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,折叠纸片,使点C与点A重合,点B落在点B′处,折痕为EF,若顶点B的坐标为(9,3),求点E、F、B′的坐标.
如图,矩形纸片AOCB,以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,折叠纸片,使点C与点A重合,点B落在点B′处,折痕为EF,若顶点B的坐标为(9,3),求点E、F、B′的坐标. 已知:如图,AB=AC,点D是BC的中点,AD=AE,AE⊥BE,垂足为E,连结DE.
已知:如图,AB=AC,点D是BC的中点,AD=AE,AE⊥BE,垂足为E,连结DE.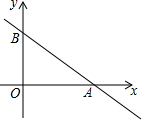 如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.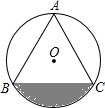 如图,已知边长为6的等边△ABC内接于⊙O.
如图,已知边长为6的等边△ABC内接于⊙O.