题目内容
10.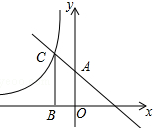 如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )
如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )| A. | y=$\frac{3}{x}$ | B. | y=-$\frac{3}{x}$ | C. | y=$\frac{3}{2x}$ | D. | y=-$\frac{3}{2x}$ |
分析 先求出点A的坐标,然后表示出AO、BO的长度,根据AO=2BO,求出点C的横坐标,代入直线解析式求出纵坐标,用待定系数法求出反比例函数解析式.
解答 解:∵直线y=-x+2与y轴交于点A,
∴A(0,2),即OA=2,
∵AO=2BO,
∴OB=1,
∴点C的横坐标为-1,
∵点C在直线y=-x+2上,
∴点C(-1,3),
∴反比例函数的解析式为:y=-$\frac{3}{x}$.
故选:B.
点评 本题考查的是反比例函数与一次函数的交点问题,根据题意确定点C的横坐标并求出纵坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.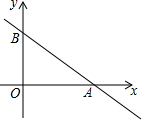 如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
 如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
19.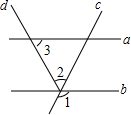 如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )
如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )
 如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )
如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
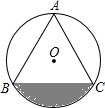 如图,已知边长为6的等边△ABC内接于⊙O.
如图,已知边长为6的等边△ABC内接于⊙O.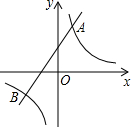 已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2)
已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2)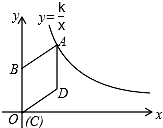 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).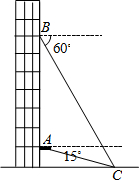 从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)
从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)