题目内容
8.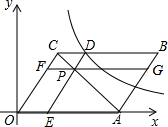 如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数$y=\frac{k}{x}$的图象经过点D,四边形BCFG的面积为8,则k的值为( )
如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数$y=\frac{k}{x}$的图象经过点D,四边形BCFG的面积为8,则k的值为( )| A. | 16 | B. | 20 | C. | 24 | D. | 28 |
分析 根据图形可得,△CPF与△CPD的面积相等,△APE与△APG的面积相等,四边形BCFG的面积为8,点C(3,4),可以求得点D的坐标,从而可以求得k的值.
解答 解:由图可得,${S}_{△AOC}={S}_{△ABC}=\frac{1}{2}$S?ABCD,
又∵S△FCP=S△DCP且S△AEP=S△AGP,
∴S?OEPF=S?BGPD,
∵四边形BCFG的面积为8,
∴S?CDEO=S?BCFG=8,
又∵点C的纵坐标是4,则?CDOE的高是4,
∴OE=CD=$\frac{8}{4}=2$,
∴点D的横坐标是5,
即点D的坐标是(5,4),
∴4=$\frac{k}{5}$,解得k=20,
故选B.
点评 本题考查反比例函数系数k的几何意义、平行四边形的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
19.已知菱形ABCD的一边为10cm,则它的周长是( )
| A. | 10cm | B. | 20cm | C. | 30cm | D. | 40cm |
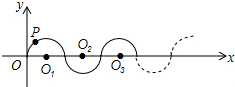 如图,在平面直角坐标系中,半径均为1各单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是(2015,-1).
如图,在平面直角坐标系中,半径均为1各单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是(2015,-1).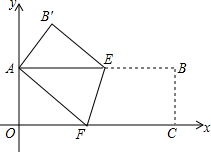 如图,矩形纸片AOCB,以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,折叠纸片,使点C与点A重合,点B落在点B′处,折痕为EF,若顶点B的坐标为(9,3),求点E、F、B′的坐标.
如图,矩形纸片AOCB,以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,折叠纸片,使点C与点A重合,点B落在点B′处,折痕为EF,若顶点B的坐标为(9,3),求点E、F、B′的坐标. 已知:如图,AB=AC,点D是BC的中点,AD=AE,AE⊥BE,垂足为E,连结DE.
已知:如图,AB=AC,点D是BC的中点,AD=AE,AE⊥BE,垂足为E,连结DE. 如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2017秒时,点P的坐标是(2017,1).
如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2017秒时,点P的坐标是(2017,1).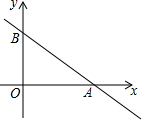 如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.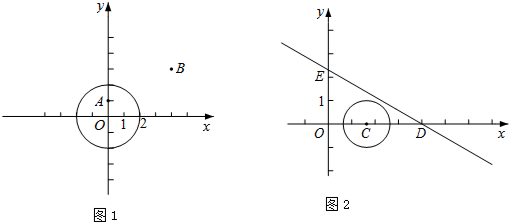
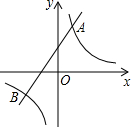 已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2)
已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2)