题目内容
9.(1)计算:$\frac{1}{\sqrt{3}}-\root{3}{8}$+|2-$\sqrt{3}$|;(2)当关于x的方程x2-2x+c=0有实数根时,求c的取值范围.
分析 (1)原式第一项分母有理化,第二项利用立方根定义计算,最后一项利用绝对值的代数意义化简,计算即可得到结果;
(2)根据方程有实数根,得到根的判别式大于等于0,即可求出c的范围.
解答 解:(1)原式=$\frac{\sqrt{3}}{3}$-2+2-$\sqrt{3}$=-$\frac{2\sqrt{3}}{3}$;
(2)∵关于x的方程x2-2x+c=0有实数根,
∴△=4-4c≥0,
解得:c≤1,
则c的范围为c≤1.
点评 此题考查了实数的运算,以及根的判别式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
19.已知菱形ABCD的一边为10cm,则它的周长是( )
| A. | 10cm | B. | 20cm | C. | 30cm | D. | 40cm |
20.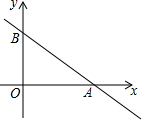 如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
 如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
19.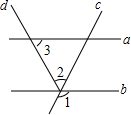 如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )
如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )
 如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )
如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
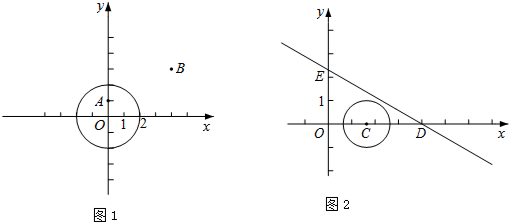
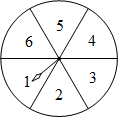 如图,转盘被等分成6个扇形,每个扇形上依次标有数字1,2,3,4,5,6.在游戏中特别规定:当指针指向边界时,重新转动转盘.
如图,转盘被等分成6个扇形,每个扇形上依次标有数字1,2,3,4,5,6.在游戏中特别规定:当指针指向边界时,重新转动转盘.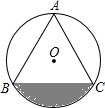 如图,已知边长为6的等边△ABC内接于⊙O.
如图,已知边长为6的等边△ABC内接于⊙O.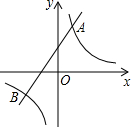 已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2)
已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2)