题目内容
17.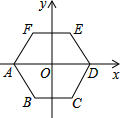 如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若点A的坐标为(-2,0),则点E的坐标为(1,$\sqrt{3}$).
如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若点A的坐标为(-2,0),则点E的坐标为(1,$\sqrt{3}$).
分析 先连接OE,由于正六边形是轴对称图形,并设EF交Y轴于G,那么∠GOE=30°;在Rt△GOE中,则GE=1,OG=$\sqrt{3}$.即可求得E的坐标.
解答  解:连接OE,由正六边形是轴对称图形知:
解:连接OE,由正六边形是轴对称图形知:
在Rt△OEG中,∠GOE=30°,OE=2.
∴GE=1,OG=$\sqrt{3}$
∴E(1,$\sqrt{3}$),
故答案为(1,$\sqrt{3}$).
点评 本题利用了正六边形的对称性,直角三角形30°的角所对的边等于斜边的一半,勾股定理等知识,求出GE和OG的长是关键.

练习册系列答案
相关题目
5.如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是( )
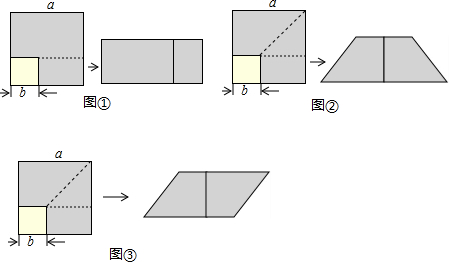

| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
2.不等式组$\left\{\begin{array}{l}{3x-1≥5}\\{2x+4<x+7}\end{array}\right.$的解集为( )
| A. | x≥2 | B. | x<3 | C. | 2≤x<3 | D. | x>3 |




 如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,BE∥DF,AD∥BC.求证:AD=BC.
如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,BE∥DF,AD∥BC.求证:AD=BC. 如图,在矩形ABCD中,BE⊥AC于点E,DF⊥AC于点F,如果AE=1,EF=2,那么FC的长度是1,AB的长度是2.
如图,在矩形ABCD中,BE⊥AC于点E,DF⊥AC于点F,如果AE=1,EF=2,那么FC的长度是1,AB的长度是2.