题目内容
9. 如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,BE∥DF,AD∥BC.求证:AD=BC.
如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,BE∥DF,AD∥BC.求证:AD=BC.
分析 根据BE∥DF,AD∥BC,得到∠BEC=∠DFA,∠A=∠C,根据AE=CF,得到AF=CE,根据ASA证出△ADF≌△CBE即可.
解答 证明:∵BE∥DF,AD∥BC,
∴∠BEC=∠DFA,∠A=∠C,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵在△ADF和△CBE中,
$\left\{\begin{array}{l}{∠A=∠C}\\{AF=CE}\\{∠BEC=∠DFA}\end{array}\right.$,
∴△ADF≌△CBE(ASA),
∴AD=BC.
点评 本题考查了平行线的性质和全等三角形的性质和判定的应用,判定两三角形全等的方法有:SAS、ASA、AAS、SSS.

练习册系列答案
相关题目
20.黄冈市地处湖北省东部,大别山南麓,长江北岸,下辖一区七县两市,总人口740万人,人口总数用科学记数法表示为( )
| A. | 70.4×105人 | B. | 7.4×106人 | C. | 7.4×105人 | D. | 7.4×104人 |
1.有一个底面半径为3cm,母线长10cm的圆锥,则其侧面积是( )
| A. | 30cm2 | B. | 30πcm2 | C. | 15πcm2 | D. | 15cm2 |
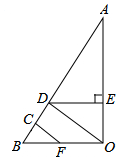 如图,已知:DE⊥AO于点E,BO⊥AO于点O,∠CFB=∠EDO,
如图,已知:DE⊥AO于点E,BO⊥AO于点O,∠CFB=∠EDO,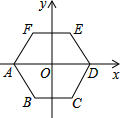 如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若点A的坐标为(-2,0),则点E的坐标为(1,$\sqrt{3}$).
如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若点A的坐标为(-2,0),则点E的坐标为(1,$\sqrt{3}$).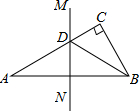 如图,在△ABC中,∠C=90°,AC=18cm,AB的垂直平分线MN交AC于D,连结BD,若$\frac{CB}{DB}=\frac{3}{5}$,则BC的长是( )
如图,在△ABC中,∠C=90°,AC=18cm,AB的垂直平分线MN交AC于D,连结BD,若$\frac{CB}{DB}=\frac{3}{5}$,则BC的长是( )