题目内容
12.在同一坐标系内,表示函数y=kx+b与y=$\frac{kb}{x}$(k≠0,b≠0)的图象是下面中的( )| A. |  | B. |  | C. |  | D. |  |
分析 根据一次函数的图象与系数的关系,由一次函数y=kx+b图象分析可得k、b的符号,进而可得k•b的符号,从而判断y=$\frac{kb}{x}$的图象是否正确,进而比较可得答案.
解答 解:根据一次函数的图象分析可得:
A、由一次函数y=kx+b图象可知k<0,b>0;y=$\frac{kb}{x}$的图象可知kb>0,与一次函数kb<0矛盾,故此选项错误;
B、由一次函数y=kx+b图象可知k>0,b>0;即kb>0,与y=$\frac{kb}{x}$的图象可知kb>0一致,故此选项正确;
C、由一次函数y=kx+b图象可知k>0,b<0;即kb<0,与y=$\frac{kb}{x}$的图象可知kb>0矛盾,故此选项错误;
D、由一次函数y=kx+b图象可知k>0,b>0;即kb>0,与y=$\frac{kb}{x}$的图象可知kb>0矛盾,故此选项错误.
故选:B.
点评 此题主要考查了一次函数图象及反比例函数的图象,
注意:一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.若m是169的算术平方根,n是121的负的平方根,则(m+n)2的平方根为( )
| A. | 2 | B. | 4 | C. | ±2 | D. | ±4 |
20.黄冈市地处湖北省东部,大别山南麓,长江北岸,下辖一区七县两市,总人口740万人,人口总数用科学记数法表示为( )
| A. | 70.4×105人 | B. | 7.4×106人 | C. | 7.4×105人 | D. | 7.4×104人 |
7.将抛物线y=x2平移得到抛物线y=x2-4,下列平移正确的是( )
| A. | 向上平移4个单位 | B. | 向下平移4个单位 | C. | 向左平移4个单位 | D. | 向右平移4个单位 |
1.有一个底面半径为3cm,母线长10cm的圆锥,则其侧面积是( )
| A. | 30cm2 | B. | 30πcm2 | C. | 15πcm2 | D. | 15cm2 |
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则比较下列大小:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则比较下列大小: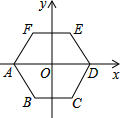 如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若点A的坐标为(-2,0),则点E的坐标为(1,$\sqrt{3}$).
如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若点A的坐标为(-2,0),则点E的坐标为(1,$\sqrt{3}$).