题目内容
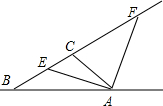 在△ABC中,∠ACB-∠B=90°,∠BAC的角平分线交BC于E,△BAC的外角平分线交BC于F,证明:AE=AF.
在△ABC中,∠ACB-∠B=90°,∠BAC的角平分线交BC于E,△BAC的外角平分线交BC于F,证明:AE=AF.考点:等腰直角三角形
专题:证明题
分析:由AE平分∠BAC,AF是△BAC的外角的平分线得到∠EAF=∠EAC+∠CAF=
(∠BAC+∠CAD)=90°,然后根据三角形的内角和与三角形外角的性质即可得到∠AFE=45°,进而得到AE=AF.
| 1 |
| 2 |
解答:证明:∵AE平分∠BAC,AF是△BAC的外角的平分线,
∴∠EAF=∠EAC+∠CAF=
(∠BAC+∠CAD)=90°,
∴△EAF是直角三角形,
∵∠ACB-∠B=90°,
∴∠BAC=180°-∠ACB-∠B=180°-(90°+∠B)-∠B=90°-2∠B,
∴∠BAE=
∠BAC=45°-∠B,
∴∠AEC=∠BAE+∠B=45°,
∴∠AFE=45°,
∴∠AEC=∠AFE,
∴AE=AF.
∴∠EAF=∠EAC+∠CAF=
| 1 |
| 2 |
∴△EAF是直角三角形,
∵∠ACB-∠B=90°,
∴∠BAC=180°-∠ACB-∠B=180°-(90°+∠B)-∠B=90°-2∠B,
∴∠BAE=
| 1 |
| 2 |
∴∠AEC=∠BAE+∠B=45°,
∴∠AFE=45°,
∴∠AEC=∠AFE,
∴AE=AF.
点评:考查了三角形的外角平分线的性质和等腰直角三角形的性质,关键是结合图形进行角的关系的推理.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 已知,如图所示,在△ABC中,AB=AC,D是△ABC内一点,试证明:
已知,如图所示,在△ABC中,AB=AC,D是△ABC内一点,试证明: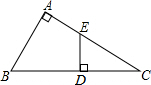 如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:AE=ED.
如图,在Rt△ABC中,∠A=90°,点D为斜边BC上一点,且BD=BA,过点D作BC的垂线交AC于点E.求证:AE=ED. 如图,在△ABC中,已知∠B=60°,∠C=45°,AB=2
如图,在△ABC中,已知∠B=60°,∠C=45°,AB=2