题目内容
已知二次函数y=ax2+bx+c（a≠0）的顶点坐标（-2，-3.2），则关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=1.3和x2= ．
考点：抛物线与x轴的交点
专题：
分析：根据函数图象与x轴的交点的横坐标关于对称轴对称，可得答案．
解答：解：已知二次函数y=ax2+bx+c（a≠0）的顶点坐标（-2，-3.2），
对称轴是x=-2，
x1与x2关于x=-2对称，
=-2，
解得x2=-5.3．
故答案为：-5.3．
对称轴是x=-2，
x1与x2关于x=-2对称，
| x2+x1 |
| 2 |
解得x2=-5.3．
故答案为：-5.3．
点评：本题考查了抛物线与x轴的交点，利用了函数图象与x轴的交点的横坐标关于对称轴对称．
练习册系列答案
相关题目
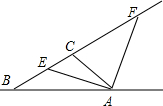在△ABC中，∠ACB-∠B=90°，∠BAC的角平分线交BC于E，△BAC的外角平分线交BC于F，证明：AE=AF．
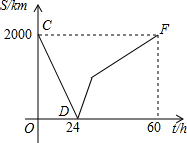如图所示，一列快车从甲地开往乙地，一列慢车从乙地开往甲地，两车同时出发，设慢车行驶时间为t小时，两车之间的距离为s千米，图中折线表示s与t之间的函数关系，当两车距离不超过200千米，两车可用车载电话通话，则两车可用车载电话通话的时间是