题目内容
 已知,如图所示,在△ABC中,AB=AC,D是△ABC内一点,试证明:
已知,如图所示,在△ABC中,AB=AC,D是△ABC内一点,试证明:| 1 |
| 2 |
考点:等腰三角形的性质,三角形三边关系
专题:证明题
分析:延长BD交AC于E.在△ABE与△CDE中,利用三角形三边关系定理得出AB+AE>BD+DE①,DE+EC>CD②,①+②,得到AB+AC+DE>BD+CD+DE,再将AB=AC代入,利用不等式的性质即可证明
(BD+DC)<AB.
| 1 |
| 2 |
解答:证明: 如图,延长BD交AC于E.
如图,延长BD交AC于E.
在△ABE中,AB+AE>BD+DE①,
在△CDE中,DE+EC>CD②,
①+②,得AB+AC+DE>BD+CD+DE,
∵AB=AC,
∴2AB>BD+CD,
∴
(BD+DC)<AB.
 如图,延长BD交AC于E.
如图,延长BD交AC于E.在△ABE中,AB+AE>BD+DE①,
在△CDE中,DE+EC>CD②,
①+②,得AB+AC+DE>BD+CD+DE,
∵AB=AC,
∴2AB>BD+CD,
∴
| 1 |
| 2 |
点评:本题考查了三角形三边关系定理:三角形两边之和大于第三边.同时考查了等腰三角形的性质及不等式的性质.

练习册系列答案
相关题目
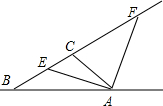 在△ABC中,∠ACB-∠B=90°,∠BAC的角平分线交BC于E,△BAC的外角平分线交BC于F,证明:AE=AF.
在△ABC中,∠ACB-∠B=90°,∠BAC的角平分线交BC于E,△BAC的外角平分线交BC于F,证明:AE=AF.