题目内容
8.等腰三角形的周长为40cm,写出腰长y关于底边长x的函数关系式0<x<20.(写出自变量的取值范围)分析 根据等腰三角形的腰长=(周长-底边长)÷2,可得出函数关系式,再根据三角形三边的关系确自变量的取值范围即可.
解答 解:由题意得:y=$\frac{40-x}{2}$,
即y=-$\frac{1}{2}$x+20,则x>0,
又∵2y>x,
∴40-x>x,
∴x<20,
即可得自变量的取值范围为:0<x<20.
故答案为:0<x<20.
点评 本题考查了根据实际问题列一次函数关系式,等腰三角形的性质及三角形三边关系,根据三角形三边关系求得x的取值范围是解答本题的关键,难度一般.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.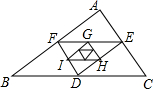 如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
 如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{1}{{2}^{n+1}}$ | D. | $\frac{1}{{2}^{n+2}}$ |
18.代数式x2-kx$+\frac{25}{4}$是一个完全平方式,则k的取值为( )
| A. | 5 | B. | $\frac{5}{2}$ | C. | $±\frac{5}{2}$ | D. | ±5 |
 如图,△ABC中,点D、E在边BC上,且△ADE是等边三角形,∠BAC=120°,求证:DE2=BD•CE.
如图,△ABC中,点D、E在边BC上,且△ADE是等边三角形,∠BAC=120°,求证:DE2=BD•CE.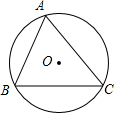 如图,⊙O是△ABC的外接圆,⊙O的半径是R=2,sinA=0.8,则弦BC的长为3.2.
如图,⊙O是△ABC的外接圆,⊙O的半径是R=2,sinA=0.8,则弦BC的长为3.2.