题目内容
18．
如图，△ABC中，点D、E在边BC上，且△ADE是等边三角形，∠BAC=120°，求证：DE2=BD•CE．
分析 根据等边三角形的性质得到AD=AE=DE，∠ADE=∠AED=60°，由邻补角的定义得到∠ADB=∠AEC=120°，求得∠B=∠CAE，根据相似三角形的性质得到$\frac{AD}{CE}=\frac{BD}{AE}$，等量代换即可得到结论．
解答 证明：∵△ABC是等边三角形，
∴AD=AE=DE，∠ADE=∠AED=60°，
∴∠ADB=∠AEC=120°，
∵∠BAC=120°，
∴∠B+∠BAD=∠BAD+∠CAE=60°，
∴∠B=∠CAE，
∴△ABD∽△CAE，
∴$\frac{AD}{CE}=\frac{BD}{AE}$，
∴AD•AE=CE•BD，
∴DE2=BD•CE．
点评 本题考查了相似三角形的判定和性质，等边三角形的性质，熟练掌握相似三角形的判定定理是解题的关键．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
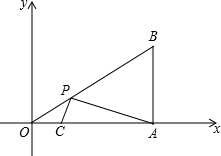如图，在平面直角坐标系中，Rt△AOB的顶点A在x轴的正半轴上，顶点B的坐标为（3，$\sqrt{3}$），∠OAB=90°，点C的坐标为（$\frac{1}{2}$，0），P为斜边OB上一个动点，求△PAC的周长的最小值．
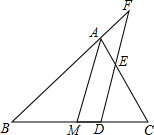如图．△ABC中，AM为BC边上中线，D为BC边上一点，过D作DF∥AM交AC于E．交BA延长线于F，求证：AB：AF=AC：AE．
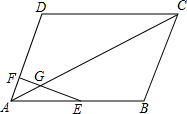如图，?ABCD中，E为AB中点，G为AC上一点，AG：GC=1：5，连接EC并延长交AD于点F．求$\frac{AF}{FD}$的值．