题目内容
19.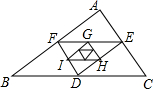 如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{1}{{2}^{n+1}}$ | D. | $\frac{1}{{2}^{n+2}}$ |
分析 根据三角形的中位线平行于第三边且等于第三边的一半,可得后一个三角形的周长等于前一个三角形的周长的一半,根据此规律进行解答.
解答 解:∵△ABC的周长为1,△DEF的顶点分别是△ABC各边的中点,
∴P2=$\frac{1}{2}$P1=$\frac{1}{2}$×1=$\frac{1}{2}$,
同理:P3=$\frac{1}{2}$P2=$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{{2}^{2}}$,
…
以此类推,Pn=$\frac{1}{2}$Pn-1=$\frac{1}{{2}^{n}}$.
故选:B.
点评 本题考查了三角形的中位线定理,推出后一个三角形的周长等于前一个三角形周长的一半是解题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
11.若关于x的方程x+$\frac{2}{x}$=c+$\frac{2}{c}$的根为x1=c,x2=$\frac{2}{c}$,则关于x的方程x+$\frac{2}{x-1}$=a+$\frac{2}{a-1}$的根是( )
| A. | x1=a,x2=$\frac{2}{a-1}$ | B. | x1=a-1,x2=$\frac{2}{a-1}$ | C. | x1=a,x2=$\frac{a+1}{a-1}$ | D. | x1=a,x2=$\frac{a}{a-1}$ |
9.无论x取何值,下列不等式总是成立的是( )
| A. | x+5>0 | B. | x+5<0 | C. | -(x+5)2<0 | D. | (x+5)2≥0 |
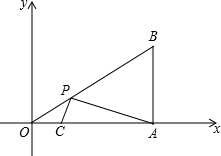 如图,在平面直角坐标系中,Rt△AOB的顶点A在x轴的正半轴上,顶点B的坐标为(3,$\sqrt{3}$),∠OAB=90°,点C的坐标为($\frac{1}{2}$,0),P为斜边OB上一个动点,求△PAC的周长的最小值.
如图,在平面直角坐标系中,Rt△AOB的顶点A在x轴的正半轴上,顶点B的坐标为(3,$\sqrt{3}$),∠OAB=90°,点C的坐标为($\frac{1}{2}$,0),P为斜边OB上一个动点,求△PAC的周长的最小值.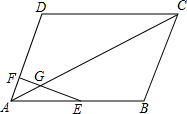 如图,?ABCD中,E为AB中点,G为AC上一点,AG:GC=1:5,连接EC并延长交AD于点F.求$\frac{AF}{FD}$的值.
如图,?ABCD中,E为AB中点,G为AC上一点,AG:GC=1:5,连接EC并延长交AD于点F.求$\frac{AF}{FD}$的值.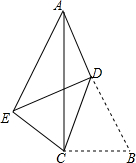 如图,在△ABC中,∠ACB=90°,BC=4,AB=10,点D是AB上的一点,将△DBC沿着CD折叠,此时点B与点E重合,连接AE,当D为AB的中点时,AE=$\frac{34}{5}$.
如图,在△ABC中,∠ACB=90°,BC=4,AB=10,点D是AB上的一点,将△DBC沿着CD折叠,此时点B与点E重合,连接AE,当D为AB的中点时,AE=$\frac{34}{5}$.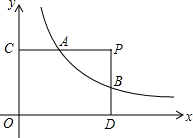 如图,点P(a,b)在第一象限内,PC⊥y轴于点C,PD⊥x轴于点D,两条垂线交反比例函数y=$\frac{k}{x}$的图象于点A、B.
如图,点P(a,b)在第一象限内,PC⊥y轴于点C,PD⊥x轴于点D,两条垂线交反比例函数y=$\frac{k}{x}$的图象于点A、B.