题目内容
7.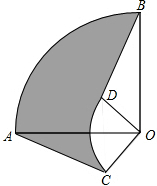 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC、BD,若OA=6cm,OC=2cm,则阴影部分的面积为8πcm2.
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC、BD,若OA=6cm,OC=2cm,则阴影部分的面积为8πcm2.
分析 根据条件可证明△AOC≌△BOD,可知S阴影=S扇形OAB-S扇形OCD,可求得答案.
解答 解:∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
在△AOC和△BOD中
$\left\{\begin{array}{l}{OA=OB}\\{∠AOC=∠BOD}\\{CO=DO}\end{array}\right.$,
∴△AOC≌△COD(SAS),
∴S△AOC=S△BOD,
∴S阴影=S扇形OAB-S扇形OCD=$\frac{90π•O{A}^{2}}{360}$-$\frac{90π•O{C}^{2}}{360}$=$\frac{1}{4}$π(62-22)=8π(cm2),
故答案为:8π.
点评 本题主要考查扇形面积的计算,把阴影部分的面积转化成两个扇形面积差是解题的关键.

练习册系列答案
相关题目
17.已知△ABC中,tanA=$\frac{1}{2}$,下列说法正确的是( )
| A. | tanB=2 | B. | tanB=$\frac{1}{2}$ | C. | sinA=$\frac{2\sqrt{5}}{5}$ | D. | sinA=$\frac{\sqrt{5}}{5}$ |
12.已知二次函数y1=a(x-2)2+k中,函数y1与自变量x的部分对应值如表:
(1)求该二次函数的表达式;
(2)将该函数的图象向左平移2个单位长度,得到二次函数y2的图象,分别在y1、y2的图象上取点A(m,n1)B(m+1,n2),试比较n1与n2的大小.
| x | … | 1 | 2 | 3 | 4 | … |
| y | … | 2 | 1 | 2 | 5 | … |
(2)将该函数的图象向左平移2个单位长度,得到二次函数y2的图象,分别在y1、y2的图象上取点A(m,n1)B(m+1,n2),试比较n1与n2的大小.
16.某电信公司给顾客提供了A、B、C三种宽带上网的收费方式:
设某用户每月的上网时间为x(小时),A、B、C三种收费方式的收费金额分别为y1、y2、y3(元).
(1)分别求y1、y1、y2关于x的函数关系式,并写出相应的自变量的取值范围;
(2)请你帮该用户选择较省钱的收费方式,并说明理由.
| 收费方式 | 月使用费/元 | 包时上网时间/小时 | 超时费/(元/分钟) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| C | 120 | 不限时 |
(1)分别求y1、y1、y2关于x的函数关系式,并写出相应的自变量的取值范围;
(2)请你帮该用户选择较省钱的收费方式,并说明理由.
 在△ABC中,∠ACB=90°,DE⊥AB.
在△ABC中,∠ACB=90°,DE⊥AB. 如图:△ABC中,∠ABC和∠ACB的平分线交于F点,过F点作DE∥BC,分别交AB、AC于点D、E.求证:
如图:△ABC中,∠ABC和∠ACB的平分线交于F点,过F点作DE∥BC,分别交AB、AC于点D、E.求证: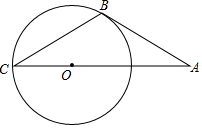 如图,直线AB是⊙O的切线,B为切点,AO的延长线交⊙O于点C,且∠A=30°,试判断AB与BC的大小关系.
如图,直线AB是⊙O的切线,B为切点,AO的延长线交⊙O于点C,且∠A=30°,试判断AB与BC的大小关系. 如图所示,有一根直立标杆,它的上部被风从B处吹折,杆顶C着地离杆底2米,修好后又被风吹折,因新断处D比前一次低0.5米,故杆顶E着地比前一次远1米,求原标杆的长度?
如图所示,有一根直立标杆,它的上部被风从B处吹折,杆顶C着地离杆底2米,修好后又被风吹折,因新断处D比前一次低0.5米,故杆顶E着地比前一次远1米,求原标杆的长度?