题目内容
12.已知二次函数y1=a(x-2)2+k中,函数y1与自变量x的部分对应值如表:| x | … | 1 | 2 | 3 | 4 | … |
| y | … | 2 | 1 | 2 | 5 | … |
(2)将该函数的图象向左平移2个单位长度,得到二次函数y2的图象,分别在y1、y2的图象上取点A(m,n1)B(m+1,n2),试比较n1与n2的大小.
分析 (1)找出顶点(2,1)代入一个点可求得二次函数的表达式;
(2)分别把A、B两点的坐标代入表达式中,求出对应的n1和n2的值,比较大小即可.
解答 解:(1)从表格看,二次函数顶点为(2,1),则k=1,
把(1,2)代入y1=a(x-2)2+1中得:2=a(1-2)2+1,a=1,
∴二次函数的表达式;y1=(x-2)2+1;
(2)由题意得:y2=(x-2+2)2+1=x2+1,
把A(m,n1)B(m+1,n2)分别代入y1、y2的表达式中,
n1=(m-2)2+1=m2-4m+5,
n2=(m+1)2+1=m2+2m+2,
n1-n2=(m2-4m+5)-(m2+2m+2)=-6m+3,
-6m+3>0,m<$\frac{1}{2}$,
-6m+3<0,m>$\frac{1}{2}$,
∴当m<$\frac{1}{2}$时,n1-n2>0,即n1>n2,
当m=$\frac{1}{2}$时,n1-n2=0,即n1=n2,
当m>$\frac{1}{2}$时,n1-n2<0,即n1<n2.
点评 本题考查了利用待定系数法求二次函数的解析式及几何变换,待定系数法就是将图象上的两点或三点的坐标代入解析式中列方程组,解出字母系数,写出二次函数的解析式;对于第二问中的纵坐标的大小比较,代入可求得.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
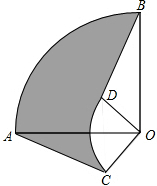 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC、BD,若OA=6cm,OC=2cm,则阴影部分的面积为8πcm2.
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC、BD,若OA=6cm,OC=2cm,则阴影部分的面积为8πcm2. 如图,E,F分别是矩形ABCD一组对边AD,CB的中点,已知矩形AEFB∽矩形ABCD,求AB:BC的值.
如图,E,F分别是矩形ABCD一组对边AD,CB的中点,已知矩形AEFB∽矩形ABCD,求AB:BC的值. 如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,DE=2cm,AB=8cm.求:⊙O的半径.
如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,DE=2cm,AB=8cm.求:⊙O的半径.